A altura de sucção positiva líquida requerida () por uma bomba pode ser expressa aproximadamente como uma função parabólica da vazão em volume. O para uma dada bomba, operando a com água, é dado por , em que de água e . Considere que o sistema de alimentação da sucção da bomba consiste em um reservatório, cuja superfície está acima da linha de centro da bomba, de uma entrada de borda-viva, de tubo de ferro fundido de de diâmetro e um cotovelo de . Calcule a vazão volumétrica máxima a , para qual a altura de carga da sucção é suficiente para operar esta bomba sem cavitação.

A equação dada:

Pode ser escrita da seguinte forma com os dados pelo enunciado:

Quando , temos:

Obtendo temos que é igual:

Sabendo que:

Temos que:

;

Do Número de Reynolds:

Sendo:

(Tabela A.7).

Temos:

Obtendo :

Com tabelado para Ferro Fundido igual a .

Com o Diagrama de Moody, obtemos o seguinte valor para :

Calculando a perda de carga que engloba a perda de carga do escoamento, do cotovelo e da entrada:

Sendo:

(Tabelado);

(Tabelado);

.

Temos:

Escreva a Equação de Bernoulli:

Fazendo as considerações do Passo 1:

Sendo:

;

;

.

Temos:

Como:

Sendo:

.

Temos:

Construa a seguinte tabela, sendo :

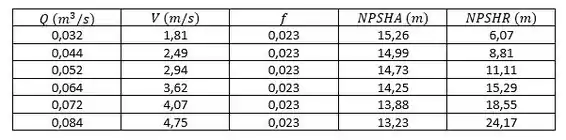
A cavitação ocorre quando se torna maior que o , e nesse caso ocorre em .