Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 102

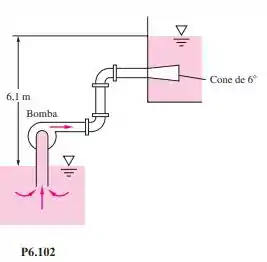
Uma bomba com rendimento de 70% fornece água a 20 ° C de um reservatório para outro 6,1 metros mais alto, como na Figura P6.102. O sistema de tubulação consiste em 18,3 m de tubo de aço galvanizado de 50 mm de diâmetro, uma entrada reentrante, dois cotovelos rosqueados de 90 ° de raio longo, uma válvula rosqueada de gaveta aberta e uma saída em canto vivo. Qual é a potência de entrada necessária em hp, com e sem uma expansão cônica bem projetada de 6 ° à saída? A vazão é 11,3 L/s.

Passo 1

Bora pra mais uma!

Para água a 20 ° C temos ρ = 998 k g m 3   e     μ = 1,002 * 10 - 3 N s m 2 . Para o aço galvanizado ε = 0,00015 m

Então ε D = 0,003 . Sem o cone de 6 ° , o coeficiente K é:

K e n t r a d a = 1 ; K c o t o v e l o s = 2 * 0,41 ; K v a l v u l a g a v e t a = 0,16 ; K s a i d a = 1

Temos que a velocidade será:

V = Q A = 0,0113 m 3 s π 0,05 m 2 4 = 5,75 m s

Daí, podemos calcular Reynolds:

R e = ρ V D μ = 998 k g m 3 * 0,05 m * 5,75 m s 1,002 * 10 - 3 N s m 2 = 286352,3

Então com a rugosidade relativa e Reynolds, podemos encontrar o fator de atrito pelo diagrama de Moody: f R e , ε D = 0,0266 . Daí

h b o m b a = ∆ z + V 2 2 g f L D + ∑ K

= 6,1 m + 5,75 m s 2 2 * 9,8 m s 2 0,0266 * 18,3 m 0,05 m + 2,242 = 2 7,55 m

Agora, calculamos a potência da bomba sem o cone:

P b o m b a = ρ g Q h b o m b a η b o m b a = 998 k g m 3 * 9,8 m s 2 * 0,0113 m 3 s * 2 7,55 m 0,7 = 4 349 , 7 W

= 5 , 92 h p .

Passo 2

Agora, vamos considerar o cone de 6 ° , neste caso o K de saída, segundo a figura 6.23 do livro, será igual a 0,3, daí:

h b o m b a = ∆ z + V 2 2 g f L D + 1 + 0,3 + 0,16 + 0,82

= 26,37 m

A potência da bomba com o difusor será:

P b o m b a = ρ g Q h b o m b a η b o m b a = 998 k g m 3 * 9,8 m s 2 * 0,0113 m 3 s * 2 6 , 37 m 0,7 = 4 220,23 W

= 5 , 7 h p .

Resposta

Sem a expansão cônica a potência necessária é de 5,92hp, com a expansão cônica 5,7hp. Uma diferença de 4%.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O efeito do arredondamento de uma saída de tubo sobre o coeficiente de perda é ( a ) desprezível, ( b ) um pouco significativo ou c muito significativo.
Um sistema de bombeamento envolve dois tubos de diâmetro diferentes (mas com comprimento, material e rugosidade iguais) conectados em série. Como você compara a as vazões e ( b ) as quedas de pressão
Um sistema de tubulação envolve dois tubos de diâmetro idênticos, mas com comprimentos diferentes conectados em paralelo. Como você compara as quedas de pressão desses dois tubos?
Durante um projeto de reajuste de um sistema de escoamento de fluido para reduzir a potência de bombeamento, é proposta a instalação de aletas nos cotovelos chanfrados, ou a substituição das curvas ag
O efeito do arredondamento de uma entrada de tubo sobre o coeficiente de perda é ( a ) desprezível, ( b ) um pouco significativo ou c muito significativo.