Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 129
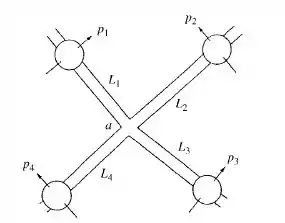
Na figura a seguir todos os quatro tubos são de ferro fundido de 45 m de comprimento e de 8 cm de diâmetro e se encontram na junção a, fornecendo água a 20°C. As pressões são conhecidas nos quatro pontos como mostrado:
Desprezando as perdas localizadas, determine a vazão em cada tubo.
Passo 1
Opa, tranquilidade aí? Bora para mais uma aventura de mecflu? Vem comigo!
Primeira coisa que vamos fazer é pegar as propriedades da água na temperatura de 20°C.
Bem, os tubos são feitos de ferro fundido, ou seja, todos eles devem possuir a mesma rugosidade , portanto a rugosidade relativa é:
Note também que todos os tubos tem .
Bem, uma metodologia muito utilizada para esse tipo de problema é: chutamos um valor de pressão no ponto de interseção dos tubos, iteramos para calcular os valores de f e vazão de tal forma que o saldo líquido de vazão na junção seja ZERO!!
Passo 2
Vamos chutar
Mas a gente sabe que por exemplo, para o tubo 1 teríamos que sua queda de pressão é igual a perda de carga causada pelo escoamento do fluido, ou seja:
Beleza, vamos fazer algo aqui já pra adiantar nossas vidas, vamos substituir já a velocidade pela vazão, beleza?
Lembrando que a velocidade pode ser substituída pela vazão pois temos que:
Vamos chutar um valor de , isso resultará em um valor de
O qual podemos calcular o valor de !
Note que agora com esse novo valor de Re e com o valor da rugosidade relativa, podemos calcular os novos valores de f no diagrama de Moody, certo? Isso é um cálculo iterativo:
- Chute
- Chute
- Calcule
- Calcule Re1
- Encontre o novo valor de f no diagrama de Moody
- Volte ao passo 3 até convergência
Para nosso tubo 1, a convergência ocorreu quando e, portanto,
Passo 3
Note que vamos ter que fazer a mesma metodologia para o tubo 2, 3 e 4 , certo? Ao final você obterá que a convergência vai te dar os seguintes valores de vazão:
Ao se somar todas as vazões na junção, devemos obter um valor muito próximo de zero:
Ou seja, o valor “próximo” de zero quem determina é você ou a questão hehe
Por exemplo, se eu chutasse um valor de , teríamos ao final um valor líquido de vazão na junta igual a -0,00296 m³/s e assim por diante.
Passo 4
Ao final, vamos tentar fazer com e seguindo a mesma metodologia de iteração abaixo:
- Chute
- Chute
- Calcule
- Calcule Re1
- Encontre o novo valor de f no diagrama de Moody
- Volte ao passo 3 até convergência
Vamos encontrar que:
Note que se você tivesse parado lá no primeiro chute que fizemos os valores de vazão estariam já muito próximos...Então novamente digo que o “quão próximo de zero” deve ser seu saldo líquido está associado ao seu critério ou o dado pelo enunciado.