Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 164
O caça de combate F16 da Força Aérea dos Estados Unidos tem uma área planiforme de asa ; ele pode desenvolver um coeficiente máximo de sustentação de . Quando totalmente carregado, sua massa é . A estrutura suporta manobras que produzem acelerações verticais de . Entretanto, os alunos pilotos estão limitados a manobras de no máximo durante o treinamento. Considere uma curva feita em voo nivelado com a aeronave inclinada. Determine a velocidade mínima na qual o piloto pode produzir uma aceleração total de no ar padrão. Calcule o raio correspondente de voo. Discuta os efeitos da altitude sobre estes resultados.
Passo 1
Nesse problema, temos o caça de combate, em que devemos encontrar a velocidade mínima na qual o piloto pode produzir de aceleração e o raio de vôo.
Para a resolução da questão, já temos alguns dados e através deles podemos fazer os cálculos:
Uma informação que devemos ter é que, assim como em casos aerodinâmicos, a força de arrasto é igual ao empuxo, por estarem na mesma direção.
Quanto a sustentação, como é uma componente perpendicular ao movimento do objeto, se iguala ao peso. Assim, temos
Passo 2
Na aceleração 5g, a força correspondente é:
Agora, a velocidade mínima corresponde ao coeficiente de elevação máximo é:
Para encontrar o raio do vôo, temos o seguinte diagrama de corpo livre:
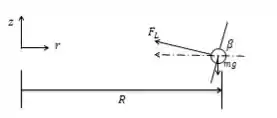
Assim, realizamos um balanço de força vertical:
Agora definimos a força horizontal igual à aceleração centrípeta:
Isolamos a aceleração centrípeta:
Pegamos a fórmula da aceleração centrípeta e podemos achar o raio do voo:
À medida que a altitude aumenta, a densidade diminui e a velocidade e o raio aumentam.
Prontinho!!!