Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 101
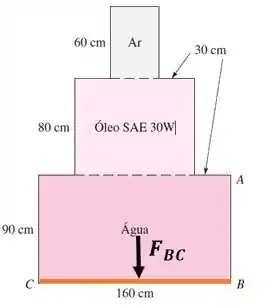
A caixa fechada em camadas da Figura P2.101 tem seções transversais quadradas horizontais em toda a sua altura. Todos os fluidos estão a 20°C. Calcule a pressão manométrica do ar se (a) a força hidrostática sobre o painel AB é de 48 kN ou (b) a força hidrostática sobre o fundo do painel BC é de 97 kN.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.7 do livro, chamada “Forças em fluidos em camadas”.
Pra entender a questão, dá uma olhada na figura do enunciado. Temos uma caixa fechada em camadas, com seções quadradas: uma preenchida com ar ( de altura) , uma preenchida com Óleo SAE 30W ( de altura) e uma com água ( de altura).
A questão quer que a gente calcule a pressão manométrica do ar para duas condições diferentes.
Pra isso, vamos utilizar o conhecimento de que para obter a resultante de uma força hidrostática em um sistema de múltiplas camadas, basta somarmos o produto da pressão de cada camada com sua respectiva área de aplicação, da seguinte forma:
Nos próximos passos eu vou mostrar como calcular a pressão de ar para uma se a força hidrostática sobre o painel AB de ou uma força hidrostática sobre o fundo do painel BC de .
Mas primeiro, vamos estabelecer aqui que os pesos específicos para óleo e para água a são, respectivamente, e .
Agora vamos lá resolver esse problema juntos!
Passo 2
Primeiro, queremos calcular a pressão do ar caso a força , agindo entre os pontos A e B da figura, tenha valor de . Para ficar mais claro, dê uma olhada na figura abaixo:
Nós temos que saber duas coisas: a primeira é que a força que queremos calcular vai agir sobre uma área específica, , que é um retângulo de altura e base . Ou seja, nosso somatório irá ser:
Em segundo lugar, devemos estabelecer que as pressões irão ser calculadas multiplicando os seus pesos específicos pelas alturas da coluna de líquido.
Para o óleo, sua coluna é de exatamente . Já para a água, essa altura será , pois a força hidrostática é horizontal, e irá agir no centro de gravidade do painel AB. Sendo assim, teremos:
Passo 3
Pra finalizar a questão, iremos calcular a pressão do ar caso a força , agindo entre os pontos B e C da figura, tenha valor de . Para ficar mais claro, dê uma olhada na figura abaixo:
Novamente, sabemos que vai agir sobre uma área específica, , que é um quadrado de lado . Ou seja, nosso somatório irá ser:
Dessa vez, todas as pressões serão calculadas em toda a extensão de suas colunas de líquido, já que esta é uma força agindo verticalmente. Sendo assim, teremos:
Pronto, matamos essa questão juntos!
Resposta
(a) A pressão manométrica do ar é
(b) A pressão manométrica do ar é