Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 125

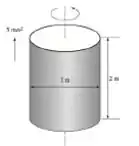
Um cilindro vertical com 1   m de diâmetro e 2   m de altura preenchido completamente com gasolina, cuja densidade é de   740   k g / m 3 . O tanque agora é posto a rodar em torno do seu eixo vertical a uma taxa de 90   r p m , enquanto é acelerado para cima a 5   m / s 2 . Determine (a) a diferença entre as pressões nos centros clas superficies inferior e superior e (b) a diferença entre as pressões no centro e na borda da superficie inferior.

Passo 1

Bom, nesse problema temos um tanque cilíndrico cheio de gasolina e girando em torno de seu eixo vertical em uma taxa especificada ao ser acelerada para cima. Dvemos determinar a diferença de pressão entre os centros inferior e superior e a diferença de pressão entre o centro e a borda da superfície inferior.

Para a resolução, vamos considerar que o aumento da velocidade de rotação é muito lento, portanto, o líquido age como um corpo rígido. Além disso, a gasolina

é uma substância incompressível.

Passo 2

Tendo o seguinte diagrama do cilindro:

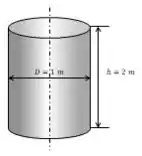
Podemos concluir que a diferença de pressão entre dois pontos 1 e 2 é P 2 - P 1 = ρ ω 2 2 r 2 2 - r 1 2 - ρ g z 2 - z 1 . Como há um efeito de aceleração linear na direção vertical substituímos g por g + a . Logo,

P 2 - P 1 = ρ ω 2 2 r 2 2 - r 1 2 - ρ g z 2 - z 1

Sabendo que D = 1 m   e D = 2 r , então, r = 0,5   m . Calculando a velocidade angular, temos:

ω = 2 π f = 2 π 90 r e v m i n × 1   m i n 60   s = 9,42   r a d / s

Passo 3

Para o item (a), tomando os pontos 1 e 2 como os centros das superfícies inferior e superior, respectivamente, temos r 1 = r 2 = 0 e z 2 - z 1 = h = 3 m . Então,

P 2 - P 1 = 0 - ρ g + a z 2 - z 1 = - ρ g + a h

Substituindo os dados:

P 2 - P 1 = - 740 k g m 3 × 9,81 m s 2 + 5 m s 2 × 2 m 1 k N 1000 k g m s 2

P 2 - P 1 = 21,9   k P a

Para o item (b), tomando os pontos 1 e 2 como o centro e a borda da superfície inferior, respectivamente, temos r 1 = 0 , r 2 = R e z 1 = z 2 = 0 . Então,

P 2 - P 1 = ρ ω 2 2 R 2 2 - 0 - 0 = ρ ω 2 R 2 2 2

Substituindo os dados:

P 2 - P 1 = 740 k g m 3 × 9,42 r a d s 2 0,5 2 2 1 k N 1000 k g m s 2

P 2 - P 1 = 8,208   k P a

Prontinho!!

Resposta

(a) 21,9   k P a

(b) 8,208   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No problema F E 2.5 , a que distância abaixo da superfície está o centro de pressão da força hidrostática??
Em líquidos “macios” (módulo de elasticidade volumétrica β baixo), pode ser necessário levar em conta a compressibilidade do líquido em cálculos hidrostáticos. Uma relação aproximada da massa específi
A válvula de retenção abaixo cobre uma abertura com diâmetro de 22,86 cm em uma parede inclinada. A articulação está a 15 cm da linha de centro, como mostrado. A válvula abrirá quando o momento na art
A comporta ABC na Figura P2.98 tem um quarto de círculo com 2,4 m de largura normal ao papel. Calcule as forças hidrostáticas horizontal e vertical sobre a comporta e a linha de ação da força resultan
O painel curvo BC da Figura P2.96 é um arco de 60°, perpendicular ao fundo em C. Se o painel tiver 4 m de largura, calcule a força hidrostática resultante da água sobre o painel.