Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 58

Calcule a profundidade e a velocidade normal do canal do Problema 11.17.

Passo 1

Beleza! Sabemos que a equação da descarga para o sistema é dada por:

Q = 1 n A R h 2 3 S b 1 2

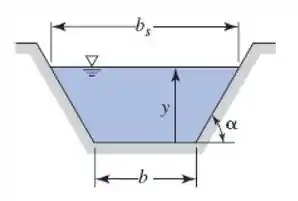
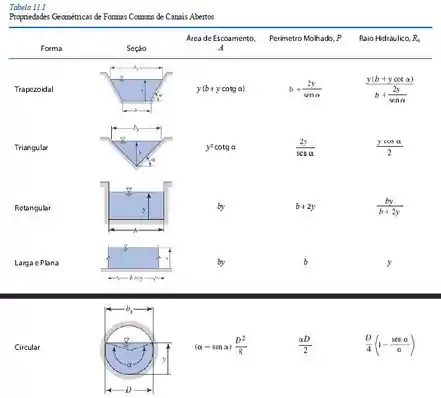
Então precisamos escrever a equação da descarga em função de y , Com o auxílio da tabela de geometria fornecida nessa seção, temos:

A = y ( b + y c o t g   α )

R h = y b + y c o t g   α b + 2 y s e n   α

Passo 2

Já temos o valor de b , e precisamos encontrar o valor de α . Como o enunciado nos disse que temos uma inclinação lateral de 1 pra 2, então, temos:

α = t g - 1 2 1 → α = 63,4 °

Substituindo os valores conhecidos nas equações para A e R h , temos:

A = y b + y c o t g   α = y ( 6 + y c o t g   63,4 ° ) → A = y ( 6 + 0,5 y )

R h = y b + y c o t g   α b + 2 y s e n   α = y 6 + y c o t g   63,4 ° 6 + 2 y s e n   63,4 ° → R h = y 6 + 0,5 y 6 + 2,237 y

Os valores da rugosidade n e da inclinação do fundo do canal foram fornecidos no enunciado, então, temos:

n = 0 , 025

S b = 0,0016

Passo 3

Então, substituindo os valores conhecidos na equação de descarga, temos:

Q = 1 n A R h 2 3 S b 1 2 → 11,3 = 1 0,025 y ( 6 + 0,5 y ) y 6 + 0,5 y 6 + 2,237 y 2 3 0,0016 1 2

7,062 = y 6 + 0,5 y y 6 + 0,5 y 6 + 2,237 y 2 3

Então, para resolver essa equação, precisamos da ajuda de uma calculadora, que nos dá:

y = 1,161   m

Passo 4

Agora, para encontrar o valor da velocidade, precisamos primeiro encontrar a área do escoamento no canal. Então vamos voltar a fórmula do passo 1:

A = y b + y c o t g   α

E, substituir os valores conhecidos:

A = 1,161 6 + 1,161 c o t g   63,4 ° → A = 7,641   m 2

Então, a velocidade pode ser encontrada através da fórmula da vazão:

Q = V A → V = Q A = 11,3 7,641 → V = 1,48   m / s

Resposta

y = 1,161   m

V = 1,48   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para um vertedor de soleira delgada sem contração C W ≈ 3,33 de comprimento b = 2,4m , P = 0,6m e H = 0,3m , determine a descarga sobre o vertedor. Despreze a velocidade de aproximação da cabeça.
Determine o coeficiente de represa para um dique com entalhe em V de 90 ° para uma carga igual a 180m m e para uma vazão de 20L / s .
A crista de um vertedor de soleira espessa está 0,3m abaixo do nível a montante do reservatório, onde a profundidade é 2,4m . Para C W ≈ 3,4 , qual é a vazão máxima por unidade de largura que poderia
Um vertedor de soleira delgada retangular com contração final tem 1,5m de comprimento. A que altura deveria a crista do vertedouro ser colocada em um canal para manter uma profundidade a montante de 2
Um vertedor de soleira delgada retangular com contração final tem 1,6m de comprimento. A que altura ele deveria ser colocado em um canal para manter uma profundidade a montante de 2,5m para uma vazão