Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 56

Considere novamente o canal semicircular do Problema 11.51. Determine a profundidade normal que corresponde a uma descarga de 0,5 m³/s.

Passo 1

Beleza! Sabemos que a equação da descarga para o sistema é dada por:

Q = 1 n A R h 2 3 S b 1 2

Então precisamos escrever a equação da descarga em função de α , para depois descobrirmos o valor da altura y . Com o auxílio da tabela de geometria fornecida nessa seção, temos:

A = α - s e n   α D 2 8

R h = D 4 1 - s e n   α α

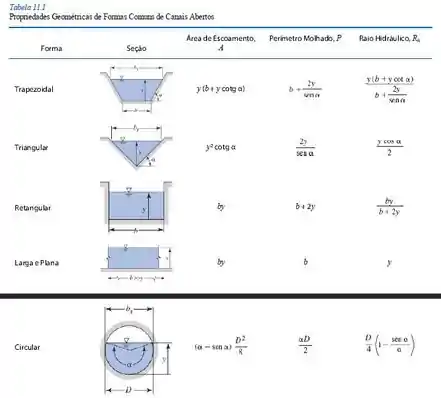
Passo 2

Substituindo os valores conhecidos nas equações para A e R h , temos:

A = α - s e n   α D 2 8 → A = α - s e n   α 8

R h = D 4 1 - s e n   α α → R h = 1 4 1 - s e n   α α

Para checar o valor da rugosidade n , vamos recorrer a tabela a seguir:

Como não temos aço corrugado, precisamos pesquisar na internet, então, adotaremos:

n = 0,02

Passo 3

Então, substituindo os valores conhecidos na equação de descarga, temos:

Q = 1 n A R h 2 3 S b 1 2 → 0,5 = 1 0,0 2 α - s e n   α 8 1 4 1 - s e n   α α 2 3 0,01 1 2

0,8 = α - s e n   α 1 4 1 - s e n   α α 2 3

Então, para resolver essa equação, precisamos da ajuda de uma calculadora, que nos dá:

α = 2,696   r a d = 154,7 °

Com isso, para encontrar a altura, basta recorrer a geometria do canal, então, teremos:

y = D 2 1 - cos ⁡ α 2 = 1 2 1 - cos ⁡ 2,696 2 → y = 0,390   m

Resposta

y = 0,390   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um escoamento em um canal retangular. Mostre que, para escoamento a uma profundidade crítica e razão de aspecto óptima b = 2 y , a vazão volumétrica e a inclinação do fundo são dadas pelas e
Um canal largo e chato, em concreto bruto, descarrega água a 1,9m 3 / s por metro de largura. Determine a inclinação crítica (a inclinação na qual a profundidade é crítica).
Um canal retangular para água pluvial, em concreto bruto, deve carregar uma vazão máxima de 2,83m 3 / s , em condição crítica. Determine a largura e a inclinação do canal.
Um canal trapezoidal forrado com tijolo tem lados inclinados de 2 : 1 e largura de fundo de 3m . Ele carrega 17m 3 / s a velocidade crítica. Determine a inclinação crítica (a inclinação na qual a prof
Um conduto retangular construído de concreto, com inclinação de 1 m por 1000 m, tem 1,8 m de largura. Água escoa a uma profundidade normal de 0,9 m. Calcule a descarga.