Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 8
8 - Uma camada horizontal de água, com espessura , tem as temperaturas de sua superfície superior e de sua superfície inferior . Determine a localização da interface sólido-líquido, em regime estacionário.
Passo 1
Suponha que a pressão ambiente seja igual à pressão atmosférica. Para a água, à pressão atmosférica, o ponto de congelamento é . Portanto, entre e , o gelo se formará.
Seja a distância entre a superfície fria e a interface sólido-líquido. Como a espessura total da camada é dada como , a distância entre a interface sólido-líquido e a superfície quente é .
Passo 2
Desenhe a rede térmica equivalente com resistências, como mostrado abaixo.
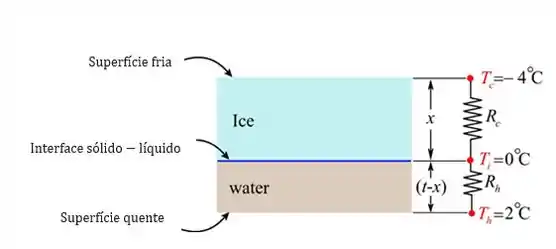
Passo 3
Para um estado estacionário, a taxa de transferência de calor por unidade de área através do gelo é igual à taxa de transferência de calor por unidade de área através da água.
Aqui é a temperatura da superfície fria, é a temperatura na interface Sólido-Líquido, é a temperatura da superfície, é a condutividade térmica do gelo e é a condutividade térmica da água.
Obtenha as propriedades do gelo na tabela A.3, “Propriedades termofísicas da água - outros materiais” do livro.
Para gelo,
Obtenha as propriedades da água na tabela A.6, “Propriedades termofísicas da água saturada” no livro didático.
Para água em , .
Passo 4
Para calcular a distância entre a interface Solido-Líquido e a superfície fria, vamos substituir pelos valores fornecidos:
Portanto, a localização da interface sólido-líquido da superfície fria é .