Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 171
171 – Repita o Prob. 3-170 usando uma placa de cobre com aletas de cobre em vez de alumínio.
Passo 1
Calcule a resistência térmica devido à condução na placa:
Aqui, a espessura de cada placa é , a condutividade térmica é , e a área perpendicular ao fluxo de calor é .
Substituindo pelos valores conhecidos, temos:
Passo 2
Calcule a resistência térmica devido à convecção da superfície da placa para o meio circundante:
Aqui, o coeficiente de transferência de calor por convecção é .
Substituindo pelos valores conhecidos, temos:
Logo a resistência total, pode ser calculada como a soma das duas resistências encontradas:
Passo 3
Calcule a temperatura da superfície de um lado da placa de circuito que NÃO está em contato com o meio.
= Temperatura do meio.
= temperatura da superfície da placa de circuito (que não está em contato com o meio).
= A taxa de calor dissipado.
Substituindo pelos valores conhecidos, temos que:
Passo 4
Calcule a temperatura da superfície da placa de circuito (que não está em contato com o meio).
= Temperatura da superfície.
= temperatura da superfície da placa de circuito (que não está em contato com o meio).
= A taxa de calor dissipado.
Substituindo pelos valores conhecidos, temos que:
Portanto, as temperaturas da superfície são
Passo 5
b)
Considere a figura a seguir, mostrando o circuito térmico:
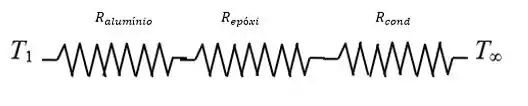
A eficiência das aletas retangulares é determinadas como:
Substituindo pelos valores conhecidos, temos que:
Calcule a eficiência das aletas retangulares da seguinte maneira:
Passo 6
Calcule o comprimento da característica para aletas retangulares.
Calcule a área da superfície aletada.
Vamos calcular a área de superfície da superfície não cortada:
Passo 7
A eficiência da aleta é definida como a razão entre a taxa real de transferência de calor da aleta e a taxa ideal de transferência de calor da aleta, se a aleta inteira estiver na temperatura base.
A taxa de transferência de calor da superfície não cortada é:
Calcule a temperatura da base para a superfície aletada.
Passo 8
Calcule a resistência térmica das aletas de cobre.
Calcule a resistência térmica do adesivo epóxi.
Passo 9
Calcule a temperatura da superfície de um lado da placa de circuito que NÃO está em contato com o meio.
Calcule a temperatura da superfície de um lado da placa de circuito que está em contato com o meio.
Portanto, neste caso, as temperaturas da superfície são e .
Resposta
Portanto, as temperaturas da superfície são .
Portanto, neste caso, as temperaturas da superfície são e .