Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 12

O campo de escoamento para um escoamento atmosférico é dado por

V → = - K y 2 π ( x 2 + y 2 ) î + K x 2 π ( x 2 + y 2 ) j ^

em que K   =   10 5   m 2 / s   e as coordenadas x e y são paralelas à latitude e longitude locais. Trace um gráfico com o módulo da velocidade ao longo do eixo x, ao longo do eixo y   e ao longo da linha y   =   x , e discuta o sentido da velocidade em relação a esses três eixos. Para cada gráfico use a faixa − 1   k m   ≤   x   ou   y   ≤   1   k m , excluindo | x |   ou   | y |   <   100   m . Determine a equação para as linhas de corrente e esboce diversas dessas linhas. O que esse campo de escoamento modela?

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Para traçarmos o gráfico, temos que no eixo x , y = 0 . Logo:

u = - K y 2 π ( x 2 + y 2 ) = 0 v = K x 2 π ( x 2 + y 2 ) = K 2 π x

Com isso, nosso gráfico fica assim:

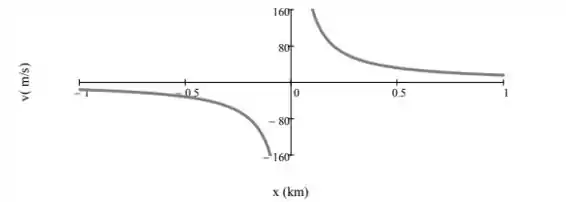
Portanto, a velocidade é perpendicular ao eixo, é muito próxima à origem e vai a 0.

Para o eixo y , onde x = 0 , temos:

u = - K y 2 π x 2 + y 2 = - K 2 π x v = K x 2 π ( x 2 + y 2 ) = 0

Logo:

Portanto, a velocidade é perpendicular ao eixo, é muito próxima à origem e vai a 0.

Por fim, para y = x , temos:

u = - K y 2 π x 2 + y 2 = - K 4 π x v = K x 2 π ( x 2 + y 2 ) = - K 4 π x

A inclinação do gráfico de y = x é 1. E a inclinação da trajetória dada por u v = - 1 . Com isso, podemos definir que a posição radial do eixo y   é   dada por:

r = x 2 + y 2 r = x 2

Então:

V = u 2 + v 2 = K 4 π   1 x 2   + 1 y 2 = K 2 π r

Logo, nosso gráfico vai ficar assim:

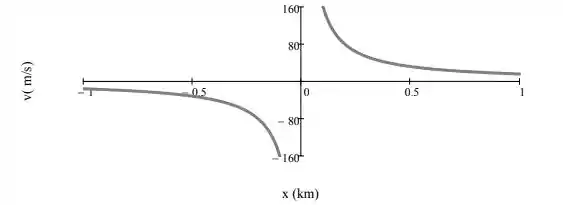
Passo 2

A segunda parte vamos encontrar a equação para as linhas de corrente. Teremos:

v u = d y d x = - K y 2 π ( x 2 + y 2 ) K x 2 π ( x 2 + y 2 ) = - x y y ∙ d y = x ∙ d x

Integrando:

y 2 2 = - x 2 2 + c x 2 + y 2 = c

Temos a equação de um círculo. Por isso, forma um conjunto de círculos concêntricos. Assim, este campo modela um fluxo de vórtice de um corpo rígido.

Resposta

A velocidade é perpendicular ao eixo, é muito próxima à origem e vai a 0.

A velocidade é perpendicular ao eixo, é muito próxima à origem e vai a 0.

x 2 + y 2 = c

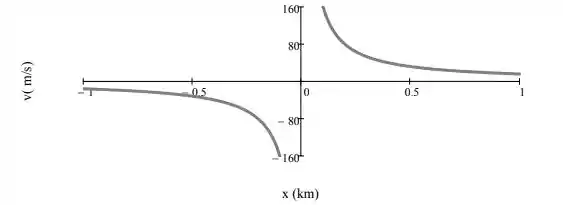
Este campo modela um fluxo de vórtice de um corpo rígido

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O campo de escoamento para um escoamento atmosférico é dado por V → = - M y 2 π î + M x 2 π j ^ î em que M=1s - 1 e as coordenadas x e y são paralelas à latitude e longitude locais. Trace um gráfico c
Considere o escoamento descrito pelo campo de velocidade V → = B x ( 1+A t ) î +C y j ^ î , com A=0,5s - 1 e B = C=1s - 1 . As coordenadas são medidas em metros. Trace a trajetória da partícula que pa
Um campo de velocidade é dado por V → =a y t î - b x j ^ î , em que a = 1s - 2 eb = 4s - 1 . Determine a equação das linhas de corrente para qualquer tempo t . Trace algumas curvas para t = 0s ,t = 1s
Um campo de escoamento é dado por V → = - q x 2 π x 2 + y 2 î - q y 2 π ( x 2 + y 2 ) j ^ î em que q=5×10 4m 2/ s . Trace um gráfico com o módulo da velocidade ao longo do eixo x, ao longo do eixo y e