Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 16
Um campo de velocidade é dado por , em que e. Determine a equação das linhas de corrente para qualquer tempo . Trace algumas curvas para ,e.
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede algumas curvas a partir da equação das linhas de corrente. Sabemos que ela é dada por:
Integrando, temos:
Passo 2
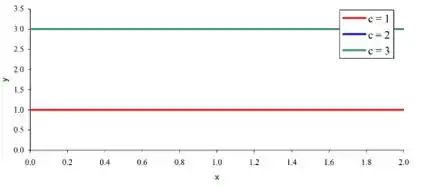
Agora, substituindo os valores de , para , temos:
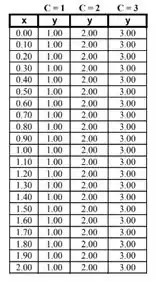
Com isso, nosso gráfico fica assim:
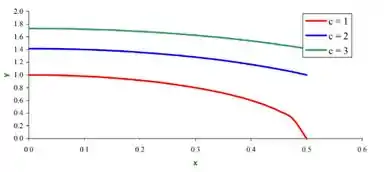
Para os outros valores de , basta repetirmos o processo. Para :
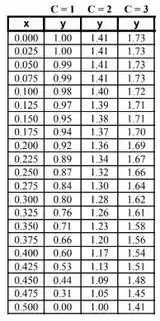
Quanto ao gráfico:
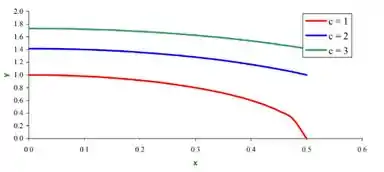
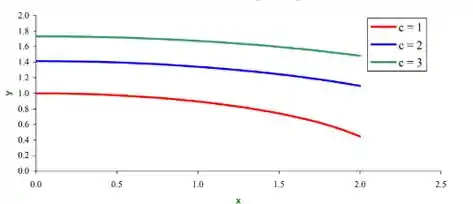
E por fim, para :
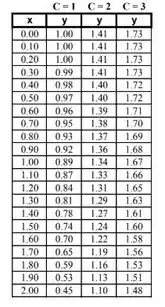
O nosso gráfico tem a seguinte cara:
Resposta
Exercícios de Livros Relacionados
ÓleoSAE30a100ºCescoaatravésdeumtubodeaçoinoxidávelcom12mmdediâmetro. Qualéagravidadeespecíficaeo peso específicodoóleo?Seoóleodescarregadodotuboencheumcilindrograduadocom100mlem9segundos,oescoamentoél
O pistão da figura levanta, com velocidade constante, um peso G = 2000N sob a ação de uma pressão. Entre o pistão e o cilindro existe uma película de lubrificante ( ρ = 800k g / m 3 ; v = 10 - 5m 2 /
O dispositivo da figura gira a 1200r p m , acionado por um motor que mantém o torque constante, independentemente da rotação. Para variar a rotação, deloca-se o mancal móvel para a esquerda. Qual a no
Ar escoando verticalmente para baixo atinge uma larga placa plana horizontal. O campo de velocidade é dado por =( a x-a y) ( 2+c o sω t ) , em que a = 5s - 1 , ω = 2 π s - 1 , x e y (medidos em metros
Considere o escoamento descrito pelo campo de velocidade V → = A ( 1+B t ) î +C t y j ^,c o mA = 1m / s î , B = 1 s - 1 eC = 1s - 2 . As coordenadas são medidas em metros. Trace a trajetória da partíc