Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas para exames de fundamentos de engenharia - Ex. 4

Para o canal do problema FE10.1, se a profundidade da água é de 2 m e a vazão de escoamento uniforme é de 24 m3/s, qual é o valor aproximado do coeficiente n de rugosidade de Manning?

(a) 0,015, (b) 0,020, (c) 0,025, (d) 0,030, (e) 0,035

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Vamos lembrar que da questão FE 10.1 a gente tinha um canal de de largura e de altura, como mostra a figura abaixo:

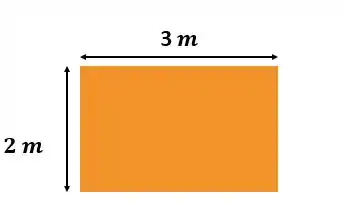
Nesse caso, temos uma vazão volumétrica , um raio hidráulico , calculado na questão FE 10.1, e uma declividade de .

Queremos descobrir o fator de Manning , e pra isso basta a gente usar a equação 10.19, dada na página 714:

Logo, a resposta do problema é alternativa (d).

Resposta

A resposta do problema é alternativa (d),

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar entra em um bocal a 30p s i a , 630R e a uma velocidade de 450p é s / s é . Considerando o escoamento isentrópico, determine a pressão e a temperatura do ar em um local onde a velocidade do ar é ig

Ar entra em um bocal a 0,2M P a , 350K e a uma velocidade de 150m / s . Considerando o escoamento isentrópico, determine a pressão e a temperatura do ar em um local onde a velocidade do ar é igual à v

Repita o Problema 12-51 para o escoamento supersônico na entrada.

Um gás ideal escoa através de uma passagem que primeiro converge e, em seguida, diverge durante um processo de escoamento adiabático, reversível e estacionário. Para o escoamento subsônico na entrada,

Ar entra em um bocal convergente-divergente a uma pressão de 1,2 MPa com velocidade desprezível. Qual é a pressão mais baixa que pode ser obtida na garganta do bocal?