Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 51
Um gás ideal escoa através de uma passagem que primeiro converge e, em seguida, diverge durante um processo de escoamento adiabático, reversível e estacionário. Para o escoamento subsônico na entrada, represente a variação da pressão, velocidade e o número de Mach, juntamente com o comprimento do bocal quando o número de Mach na área de escoamento mínimo for igual à unidade.
Passo 1
E aí! Tudo bem com você? Animado para fazer um exercício de escoamento de gás ideal em um bocal convergente-divergente?
O exercício quer saber como a pressão , a velocidade e o número de Mach de um gás variam ao longo de um bocal convergente-divergente, se na garganta do bocal. Além disso o enunciado informa que o escoamento é subsônico na entrada ( na entrada)!
Podemos separar essa questão em três partes.
- Na primeira parte, vamos entender como a velocidade varia ao longo de um bocal convergente-divergente, quando na garganta e na entrada.
- Na segunda parte, vamos entender como a pressão varia para a mesma situação.
- Na terceira parte, descobriremos como o número de Mach varia para a mesma situação.
A figura abaixo mostra as informações que temos e os dados que buscamos.
Para descobrir como varia, temos que usar a equação de conservação de massa e a equação da vazão mássica para o bocal.
onde é a vazão mássica através do bocal, é a densidade do fluido e é a área do bocal pela qual o escoamento passa.
Para descobrir como varia, temos que descobrir primeiro como a temperatura varia através da equação que relaciona a velocidade com a temperatura (equação 12-4 do livro).
é o calor específico a pressão constante do gás e é a temperatura de estagnação do gás que é igual em todos os pontos do escoamento no bocal.
Depois, usaremos a equação que relaciona a pressão com a temperatura (equação 12-5 do livro) para, enfim, descobrir como varia no bocal.
é a pressão de estagnação do gás que também é igual em todos os pontos do escoamento no bocal.
Fazemos isso, usando a equação de em função de .
onde é a velocidade do som do gás.
A velocidade do som de um gás ideal é calculada usando a equação 12-11 do livro.
onde é a razão de calores específicos do gás ideal e é a constante do gás.
Passo 2
Nesse passo vamos resolver a primeira parte do problema, descobrindo como a velocidade do fluido varia através do bocal convergente-divergente. Para isso nós vamos ter que usar a lei de conservação de massa duas vezes: uma para a parte convergente do bocal e outra para a parte divergente do bocal. A figura abaixo mostra termos importantes para usar a conservação de massa.
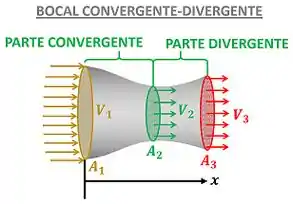
, e são as velocidades do fluido na entrada do bocal, na garganta do bocal e na saída do bocal respectivamente. , e são as áreas pela qual o fluido passa na entrada do bocal, na garganta do bocal e na saída do bocal respectivamente.
A lei de conservação de massa da parte convergente do bocal diz que a vazão mássica de na entrada do bocal deve ser igual à vazão mássica na garganta do bocal .
Reorganizando a equação final acima, achamos uma expressão para a velocidade .
Como área de entrada do bocal é maior que a área da garganta , é maior que . Ou seja, na parte convergente do bocal, a velocidade do fluido aumenta!
A lei de conservação de massa da parte divergente do bocal diz que a vazão mássica de na garganta do bocal deve ser igual à vazão mássica na saída do bocal .
Reorganizando a equação final acima, achamos uma expressão para a velocidade .
Como área da garganta do bocal é menor que a área de saída , podemos achar que o é menor que . No entanto, essa conclusão está errada! Ela não está levando em conta que o escoamento na parte divergente do bocal é supersônico. Quando o escoamento é supersônico na parte divergente, a densidade do fluido diminui muito. Logo:
Isso faz com que a velocidade fique maior que a velocidade . Ou seja, na parte divergente do bocal supersônico, a velocidade do fluido também aumenta!
Passo 3
Nesse passo vamos resolver a segunda parte da questão, descobrindo como a pressão varia através do bocal.
Para fazer isso, temos que descobrir como a temperatura do fluido varia ao longo do bocal reorganizando a equação 12-4 do livro.
é igual em todos os pontos do escoamento. Logo, é constante. Como a velocidade do fluido aumenta ao longo de todo o bocal, vemos pela equação acima que diminui ao longo de todo o bocal.
Para descobrir, enfim, como a pressão do fluido varia, temos que reorganizar a equação 12-5 do livro.
é igual em todos os pontos do escoamento. Logo, é constante. Como diminui ao longo de todo o bocal, a pressão também diminui ao longo de todo o bocal.
Passo 4
Nesse passo vamos resolver a terceira e última parte da questão, descobrindo como o número de Mach varia através do bocal.
Fazemos isso, usando a equação de em função de .
A velocidade do som de um gás ideal é calculada usando a equação 12-11 do livro.
Substituindo a expressão de na equação de :
Sabemos que a velocidade do fluido aumenta ao longo de todo o bocal. Também sabemos que a temperatura do fluido diminui ao longo de todo o bocal. Logo, o número de Mach aumenta ao longo de todo o bocal.
Resposta
A velocidade e o número de Mach do fluido aumentam ao longo de todo o bocal convergente-divergente. Já a pressão do fluido diminui ao longo de todo o bocal.