Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 14
Uma chapa metálica de 5m de comprimento está sendo transportada em uma esteira com velocidade 5m/s, enquanto o revestimento da parte superior da superfície está sendo curada por lâmpadas de infravermelho. O revestimento na superfície superior da chapa metálica tem absortividade de 0,6 e emissividade de 0,7, enquanto o ar ambiente circundante está na temperatura de 25ºC. A transferência de calor por radiação acontece apenas na superfície superior, enquanto a transferência de calor por convecção acontece por ambas as superfícies das chapa, superior e inferior. Considerando que as lâmpadas de infravermelho fornecem um fluxo de calor de 5000W/m², determine a temperatura da superfície da chapa. Avalie as propriedades do ar em 80ºC.
Passo 1
Vamos analisar primeiro o problema, ok?
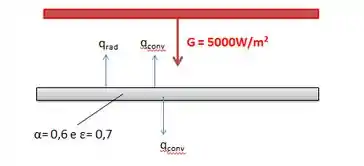
Vamos aqui entender o que acontece com a placa usando um balanço de energia:
O problema não diz nada se o problema é transiente, então podemos dizer que não haverá acúmulo de energia, assim como também não há geração de energia na placa, o que nos dá um balanço da seguinte forma:
Agora eu te pergunto, olhando para a chapa, você consegue identificar como a energia está entrando e saindo da placa?
O problema nos dá uma dica, ele diz que ocorre uma ABSORÇÃO (entra) de 60% de toda a energia que está sendo jogada na placa (G) e que ela EMITE 70% (sai) na forma de radiação e que além disso há troca de calor por convecção pelos dois lados da placa como está no desenho também (sai da placa).
Pegou a ideia? Você tem que só identificar quais são os meios que entram e saem a energia de um sólido que você consegue resolver DIVERSOS problemas desse tipo.
Passo 2
Aplicando o que foi dito no nosso balanço, temos:
Note que é uma constante.
OBS: Eu só escrevi 2qconv porque a gente tem que a temperatura da superfície superior é IGUAL a temperatura da superfície inferior e o fluido também é igual assim como sua temperatura. Se não fossem iguais as condições, você teria duas taxas convectivas DIFERENTES, ok?
Ok, mas veja só que maravilha, temos o valor de quase todas as variáveis, menos Ts que é o que desejamos e o bendito do coeficiente de transferência de calor convectivo, mas sabemos como calcular ele :D
Passo 3
Vamos agora calcular nosso coeficiente convectivo, ok?
Existe um passo-a-passo para isso porque temos várias correlações de Nusselt, então segue a dica:
- Definir se é escoamento laminar ou turbulento
- Em qual geometria o fluido está escoando
- Selecionar a correlação
- SEJA FELIZ ENCONTRANDO h
Passo 4
Primeiro, calculamos Reynold para o primeiro passo:
Onde todas as propriedades são do fluido. O problema nos diz para pegarmos essas propriedades em 80ºC. O que você teria que fazer? Procura na tabela de apêndice do livro uma que referente ao ar e suas propriedades e catar elas na temperatura correta.
OBS: Para escoamentos externos, as propriedades são sempre coletadas na temperatura de filme, que é a média aritimética entre a temperatura de superfície do sólido e do fluido (SIM, em alguns casos você vai ter que chutar a temperatura de superfície mesmo o enunciado te pedindo para calcular ela. É um método iterativo que vamos ver mais pra frente).
Substituindo, temos:
Para uma placa plana, o regime é considerado turbulento a partir de Re > 5x105... Mas para placa plana, na maioria das vezes quando temos um regime turbulente, dizemos que ele é uma combinação de regime laminar com turbulento.
Passo 5
Estamos sobre uma geometria de placa plana, então podemos tomar a seguinte correlação, onde todas as propriedades são referidas ao fluido.
Isolando h, temos:
Passo 6
Vamos agora substituir os valores no nosso balanço de energia:
Note que todos os termos na direito vão nos dar a unidade W, enquanto o termo da esquerda da igualdade nos dará uma resposta em W/m². Para termos consistência na equação, precisamos multiplicar o lado esquerdo pela área também.
Ou ainda:
Agora é só substituir os valores, beleza? Porém, note que vamos ter uma equação de 4º grau (WTF!!!), mas relaxa que isso sua calculadora faz ou um programa faz pra você! Dificilmente alguém vai mandar tu resolver esse tipo de problema na marra e na mão!
IMPORTANTE: Passa as temperaturas pra Kelvin, beleza?
Resolvendo, teremos Ts = 411K
Resposta
Ts = 411K