Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 15
O óleo de um motor a 80ºC escoa sobre uma placa plana de 12 m de comprimento e uma temperatura de 30ºC com velocidade de 2,5 m/s. Determine a força total de arrasto e a taxa de transferência de calor ao longe da placa por unidade de largura
Passo 1
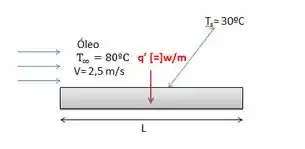
Para problemas com escoamento externo, um dos pontos principais é saber escolher em qual temperatura devemos pegar as propriedades do fluido. Elas devem ser tomadas na temperatura de filme que é a média aritmética entre a temperatura da superfície do sólido e a temperatura do fluido, ou seja, para esse caso
Vou colocar aqui pra te adiantar os valores da propriedade, ok?
Passo 2
Precisamos calcular primeiro o valor de Reynold para saber se estamos em regime turbulento ou laminar.
Podemos calcular Re das seguintes formas:
Eu prefiro usar a 2ª maneira porque são menos variáveis pra procurar na tabela de propriedades do fluido.
Para uma placa plana, o regime turbulento só acontece após Re > 5 x 105, então temos um regime laminar nesse nosso caso.
Passo 3
Vamos calcular agora a taxa de transferência de calor por largura da placa!
A gente sabe que o fluido está transferindo calor pra placa na forma convectiva, onde a equação que dita essa taxa é dada por:
A gente tem que A= LxW onde W é a largura da placa, e portanto
Mas, ok! Precisamos também encontrar o h, certo? E como fazemos isso? Correlações de Nusselt.
Para um escoamento laminar e uma geometria de placa plana, temos:
Substituindo os valores...
Agora é só a gente substituir na equação de q’ e ser feliz :D
Passo 4
Para calcular a força de arrasto total é só aplicar a fórmula, basicamente!
Agora é só substituir Cf pela equação: