Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 60

Considere um avião voando a uma velocidade de 800 km/h na altitude de 10 km, onde as condições de atmosfera padrão são -50°C e 26,5 kPa. Cada asa do avião pode ser modelada como uma placa plana de 25 m x 3 m, e o coeficiente de atrito das asas é 0,0016. Usando a analogia entre quantidade de movimento e transferência de calor, determine o coeficiente de transferência de calor para asas em condições de contorno.

Passo 1

Primeiro, vamos tirar as informações dadas pelo enunciado. Sabemos que a velocidade do ar é V = 800   k m / h (que devemos converter para m/s antes de utilizar nos cálculos) e que o ar tem propriedades iguais à da atmosfera na altitude de 10 km. Na tabela A-17 do apêndice do livro podemos consultar estas propriedades que são:

ρ = 0,414 K g m 3

μ = 1,458 x 10 - 5 k g m . s

k = 0,0201 W m . K

Também sabemos que o coeficiente de atrito é C f = 0,0016 .

Passo 2

Agora iremos verificar se podemos utilizar a analogia de Reynolds. Só para relembrarmos a analogia de Reynolds pode ser utilizada em escoamento sobre placa plana e com número de Prandtl aproximadamente 1. Se essas condições não forem atendidas, usaremos a analogia modificada de Reynolds, que se aplica a um maior número de casos. Vamos então calcular o número de Reynolds e em seguida o de Prandtl:

R e = ρ V L μ

Em que L é o comprimento no sentido do escoamento. Agora preciso que você use um pouco da sua imaginação e enxergue a imagem a seguir como sendo o nosso avião visto de cima:

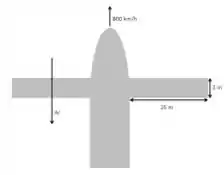
Pela figura podemos constatar que o ar escoa pelo lado L = 3   m . Substituindo os valores no número de Reynolds:

R e = 0,414 x 800 3,6 x 3 1,458 x 10 - 5

R e = 1,9 x 10 7

Agora o número de Prandtl. Sabemos que o ar está em uma pressão baixa (26,5 kPa), certo? Um gás em baixa pressão pode ser considerado como um gás ideal e, para gases ideais, P r = 1 . Então o que vamos fazer é exatamente esta consideração e assim, nosso número de Prandtl é 1 e, podemos utilizar a analogia de Reynolds.

Passo 3

A analogia de Reynolds é definida como:

C f R e 2 = N u

Como já recebemos o coeficiente de atrito no enunciado e , já calculamos R e podemos obter o número de Nusselt:

N u = 0,0016 x 1,9 x 10 7 2

N u = 15.200

Com o número de Nusselt podemos calcular o coeficiente de transferência de calor do ar:

N u = h x L k

h = N u x k L

h = 15.200 x 0,0201 3

h = 101,84 W m 2 K

Resposta

Portanto, o coeficiente convectivo para essas condições é h = 101,84 W m 2 K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11 – Considere dois casos envolvendo escoamento paralelo de ar seco com V=1m/s, T ∞ = 45 ℃ ℃, e pressão atmosférica sobre um prato isotérmico a TS=20°C. No primeiro caso, Rex,c=5x105, enquanto que no
15 – Estime a potência (W/m2) requerida para manter uma placa de latão a ΔTe=10°C enquanto água saturada a 1 atm está fervendo. Qual é a potência requerida se a água está pressurizada a 10 atm? Em qua
7 – O comportamento da histerese da curva de ebulição se torna menos pronunciada conforme a diferença entre os fluxos de calor máximo e mínimo se tornam pequenos. Calcule a razão do máximo e mínimo fl
17 – Foi demonstrado experimentalmente que o fluxo de calor critico é altamente dependente da pressão, principalmente através da dependência da pressão da tensão superficial do fluido e do calor laten
Analise detalhadamente as figuras (9.4) e (9.5) .