Um chip de silício com espessura e condutividade térmica é resfriado pela ebulição de um fluorocarboneto líquido saturado sobre sua superfície. Os circuitos eletrônicos na parte inferior do chip produzem um fluxo térmico uniforme de , enquanto os lados do chip são perfeitamente isolados.

As propriedades do fluorcarboneto saturado são e. Além disso, as constantes da ebulição nucleadas são e .

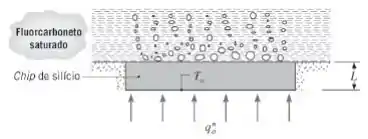
(a) Em condições de regime estacionário, qual é a temperatura na superfície inferior do chip? Se, durante a realização de testes com o chip, for aumentado para do fluxo térmico crítico, qual será o novo valor da temperatura em regime estacionário?

(b) Calcule e represente graficamente as temperaturas nas superfícies do chip (superior e inferior) como uma função do fluxo térmico para . Se a temperatura máxima admitida no chip é de , qual é o valor máximo permitido para ?

Para resolver essa questão vamos assumir:

(1) Condições em estado estacionário;

(2) Fluxo de calor uniforme e lados adiabáticos, portanto, condução unidimensional no chip;

(3) Propriedades constantes;

(4) Nucleato em ebulição no líquido.

Os balanços de energia nas superfícies superior e inferior geram,

Onde e são relacionados pela correlação de Rohsenow,

Então, para ,

Da Lei de Fourier vemos que,

Para um fluxo de calor que é do fluxo crítico de calor , temos,

Dos resultados do cálculo anterior e da correlação de Rohsenow, temos:

Então, e,