Radiação solar incide sobre a cobertura de vidro de um coletor solar a uma taxa de 700 W/m². O vidro transmite 88% da radiação incidente e tem emissividade de 0,90. A necessidade de água quente da família no verão pode ser atendida por 2 coletores de 1,2 m de altura e 1 m de largura. Os dois coletores estão ligados um ao outro de um lado, de forma que parecem um coletor de 1,2 m x 2 m de tamanho. A temperatura da tampa de vidro é medida como 35°C em um dia em que a temperatura do ar está em torno de 25°C e o vento está soprando a 30 km/h. A temperatura efetiva do céu para troca por radiação entre a tampa de vidro e o céu aberto é de -40°C. A água entra no tubo absorvedor numa vazão de 1 kg/min. Partindo do princípio que a superfície traseira da placa de absorção seja fortemente isolada e que a perda de calor só aconteça através da tampa de vidro, determine (a) a taxa total das perdas de calor a partir do coletor, (b) a eficiência do coletor, que é a razão da quantidade de calor transferido para água e a energia solar incidente sobre o coletor, e (c) o aumento da temperatura da água à medida que escoa através do coletor.
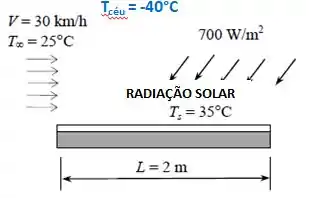
Passo 1
(a) O que se pede aqui é a taxa total de perda do coletor, que será dada por
Vamos tomar as propriedades do ar em Tf =30°C
Calculamos primeiro o valor de Reynold!
Estamos acima do Reynold crítico e portanto vamos ter um escoamento combinado
Passo 2
Calculamos h:
Passo 3
Passo 4
(b) Aqui, você precisará ter uma sacada: A energia que passa pra água é igual a diferença entre a energia incidida (G) sobre a placa e o quanto se perde dessa energia para ambiente.
Passo 5
(c) Para determinar a variação de temperatura da água, basta usar a fórmula lá do ensino médio que a gente chamava de “que macete”, se lembra?
Onde esse q se refere ao calor que foi passado para água, beleza? E é a vazão mássica de escoamento!