Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 39

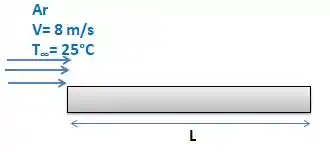
Ar a 25°C e 1 atm está escoando sobre uma placa plana com velocidade de 8 m/s. Determine a distância do bordo de ataque da placa onde o escoamento se torna turbulento e a espessura da camada limite nesse local.

Passo 1

O que você precisa primeiro lembrar nesse problema é REYNOLD CRÍTICO. A gente tem usado bastante ele nas justificativas para dizer se o escoamento é laminar ou combinado/turbulento.

Esse valor equivale ao momento em que começa a ter a transição do regime de escoamento e tem um valor fixo para placa plana que é R e x ,   c r i t c = 5   x   10 5

Vamos considerar também que a placa está em equilíbrio térmico com o ar, e, portanto as propriedades serão tomadas em Tf = 25°C

ρ = 1,184   k g / m ³

v = 1,56   x   10 - 5   m ² / s

R e x ,   c r i t i c = V X c v → R e x ,   c r i t i c   v V = X c  

5   x   10 5     x   1,56   x   10 - 5 8 = X c → X c = 0,967   m

Passo 2

A camada limite é dada pela seguinte equação:

δ x = 5 X R e x 0,5

  δ x c = 5 X c R e X c 0,5 = 5   x   0,967 5   x   10 5 0,5 = 0,007   m = 0,7   c m

OBS: Vale lembrar que essa equação que usamos para determinar a espessura da camada limite é considerando escoamento laminar, já que usamos Xc como referência para esse cálculo. Se estivéssemos em um local da placa acima de Xc, teríamos que usar uma equação de camada limite para regime turbulento, se ligou?

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Óleo de motor a 100 ° C e a uma velocidade de 0,1m / s escoa sobre as duas superfícies de uma placa plana com 1m de comprimento mantida a 20 ° C . Determine:(a) As espessuras das camadas-limite de vel
Seja o escoamento paralelo e em regime estacionário de ar atmosférico sobre uma placa plana. O ar possui uma temperatura e uma velocidade na corrente de livre de 300K e 25m / s .(a) Calcule a espessur
Considere um metal líquido ( P r ≪ 1 ) , com condições na corrente livre μ ∞ e T ∞ , escoando paralelamente sobre uma placa plana isotérmica a T s . Admitindo u = u ∞ ao longo de toda a camada-limite
Seja o escoamento laminar e paralelo em uma placa plana isotérmica de comprimento L , fornecendo um coeficiente de transferência de calor médio de h - L . Se a placa for dividida em N placas menores,
Explique sob quais condições a taxa de transferência de calor total em uma placa plana isotérmica com dimensões L × 2 L seria a mesma, independentemente do fato do escoamento paralelo sobre a placa se