Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 40
Chips, com de lado, são montados em um substrato que se encontra instalado em uma câmara cujas paredes e o ar interior são mantidos à temperatura de. Os chips têm uma emissividade e temperatura máxima permitida de.
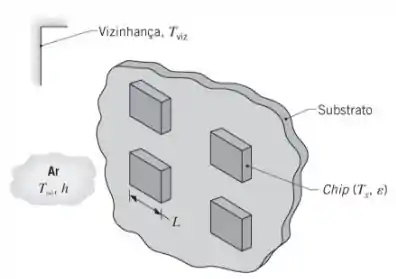
(a) Se calor é descartado pelos chips por radiação e convecção natural, qual é a potência operacional máxima de cada chip? O coeficiente convectivo depende da diferença entre as temperaturas do chip e do ar e pode ser aproximado por, sendo
(b) Se um ventilador for usado para manter o ar no interior da câmara em movimento e a transferência de calor for por convecção forçada com qual é a potência operacional máxima?
Passo 1
Vamos começar nossa questão da sequência de balanço de energia e efeitos combinados \o/. Aqui, nós temos chips eletrônicos em que nos é dado a largura, emissividade da superfície e temperatura máxima permitida. Além da temperatura do ar e arredores e o coeficiente de convecção.
A partir disso nós temos que calcular a dissipação de potência máxima para convecção livre variável e a dissipação de potência máxima para convecção forçada. Então vamos fazer algumas considerações.
Passo 2
Para resolver a questão, vamos assumir que:
- Estamos em condição de estado estacionário;
- Temos um troca de radiação entre uma superfície pequena e um compartimento grande;
- A transferência de calor dos lados do chip ou da parte traseira do chip por condução através do substrato é insignificante.
A partir das considerações acima, temos que a dissipação de energia elétrica pelo chip deve ser equilibrada pela transferência de calor por radiação e convecção. Então,
Onde a área é representada por:
Passo 3
Então, podemos calcular a letra(a), sabendo que a troca de calor por convecção é natural, da seguinte forma:
Substituindo os valore:
E para o caso da troca de calor por radiação, temos:
Então, a potência operacional máxima de cada chip é:
Passo 4
Para letra (b) a troca de calor por convecção é forçada, então:
Já a troca de calor por radiação é a mesma do caso anterior. Então potência operacional máxima é: