Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 15.Problemas - Ex. 17
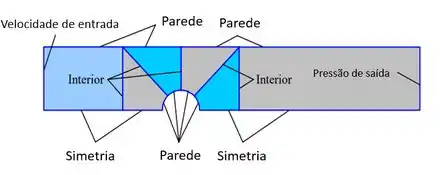
Um código CFD incompressível é usado para simular o escoamento da água através de um canal retangular bidimensional no qual existe um cilindro circular (Figura P15-17). Um escoamento turbulento com média de tempo é gerado usando um modelo de turbulência. A simetria horizontal com relação ao cilindro é considerada. O escoamento entra da esquerda e sai para a direita como mostra a figura. A velocidade de entrada V é conhecida e a pressão de saída também é conhecida. Gere o bloqueio de uma malha estruturada usando blocos de quatro lados, e represente uma malha grosseira usando células de quatro lados, tomando o cuidado de agrupar as células perto da parede. Tome cuidado também para evitar células com inclinação alta. Rotule as condições de contorno que devem ser aplicadas a cada lado de cada bloco do seu domínio computacional. (Sugestão: seis a sete blocos são suficientes.)
Passo 1
Fala aí, galerinha. Tudo beleza? Vamos fazer mais uma questão de MecFlu pra tirar aquele 10 na prova.
Neste problema devemos esboçar o bloqueio de uma grade estruturada, esboçar uma grade grosseira e rotular todas as condições de contorno a serem aplicadas ao domínio computacional.
Em primeiro lugar, reconhecemos que, por causa da simetria, podemos dividir o domínio ao meio verticalmente. Construímos quatro blocos ao redor do meio cilindro para transformar de redondo em quadrado e, em seguida, adicionamos blocos retangulares simples a montante e a jusante do cilindro. Ao todo teremos são seis blocos. Vamos ver como isso vai ficar na figura abaixo:
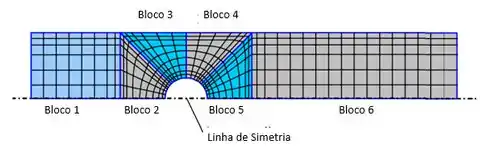
Com a estrutura de bloco acima, nenhuma célula está altamente enviesada e as células estão agrupadas perto da parede do cilindro e da parede superior do duto, conforme desejado.
Passo 2
Com isso, temos que a borda inferior do domínio computacional é uma linha de simetria. A entrada é uma entrada de velocidade. Temos uma saída de pressão. A borda superior do domínio computacional é uma parede. As arestas que definem o cilindro também são paredes.
Finalmente, existem 5 arestas que são especificadas como interiores. Todos eles estão identificados:
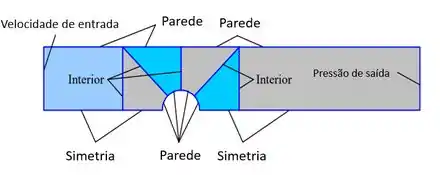
É isso, galera. Bora pra praticar mais pra ficar craque.
Resposta
