Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 15.Problemas - Ex. 32
Repita o Problema 15-31, exceto pelo uso de uma malha triangular não estruturada, mantendo todo o restante igual. Você obtém os mesmos resultados do Problema 15-31? Compare e discuta.
Passo 1
Fala aí, galerinha. Tudo beleza? Vamos fazer mais uma questão de MecFlu pra tirar aquele na prova. Neste problema devemos gerar soluções CFD para fluxo externo sobre um bloco cilíndrico. Especificamente, devemos comparar o coeficiente de arrasto para vários valores de (a extensão do limite externo do domínio computacional). Além disso, devemos comparar o valor calculado de CD com o Valor experimental.
Neste caso, temos um escoamento incompressível, axissimétrico em relação ao eixo e turbulento, mas constante na média. Dado que e , o número de Reynolds com base no diâmetro do cilindro é:
E os valores experimentais indicam que o coeficiente de arrasto para este corpo é em números de Reynolds maiores que .
Passo 2
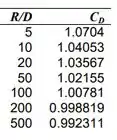
Então, o código CFD é executado para oito valores de , todos os outros sendo iguais. é tabulado como uma função de na tabela abaixo:
E plotado assim:
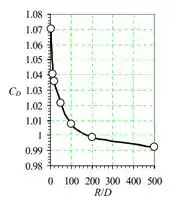
Conforme a extensão do domínio computacional cresce em tamanho, o coeficiente de arrasto diminui continuamente, mas está tentando nivelar por . Assim, uma extensão de domínio computacional de ou mais é necessária para alcançar a independência de . Relatamos um valor final de . Infelizmente, o programa não permite valores maiores que .
Passo 3
Existem várias razões possíveis para a discrepância entre o valor calculado de e o valor obtido experimentalmente de (cerca de ). Em primeiro lugar, o fluxo real é provavelmente instável, com vórtices sendo lançados na esteira, enquanto estamos simulando um fluxo constante.
Além disso, o derramamento instável de vórtices torna o fluxo não mais simétrico em relação ao eixo , enquanto estamos forçando nosso fluxo a ser simétrico em relação ao eixo. Além disso, a resolução da rede pode não ser adequada para alcançar a independência da rede.
Finalmente (e mais importante), estamos usando um modelo de turbulência para simular este campo de fluxo. A solução CFD que obtemos é tão boa quanto o grau em que o modelo de turbulência modela corretamente a física da turbulência. Conforme discutido no texto, nenhum modelo de turbulência é universalmente válido para todos os tipos de fluxos turbulentos.
As discrepâncias entre o experimento e o CFD sempre existirão, independentemente de quão fina seja a grade ou quão grande seja a extensão do domínio computacional.
Passo 4
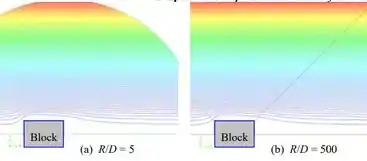
Assim, linhas aerodinâmicas próximas ao corpo são plotadas para e :
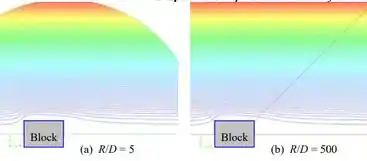
Há surpreendentemente pouca diferença observável entre esses dois casos extremos. Comparado com o caso , parece que o caso axissimétrico requer uma extensão de domínio computacional maior. Isso é surpreendente, porque em um campo de fluxo axissimétrico, o fluido pode fluir ao redor do corpo em todas as direções, não apenas na parte superior e inferior como no fluxo . À medida que o fluido se afasta do corpo, o raio também aumenta ali, e mais massa pode fluir através dessa localização radial em comparação com o caso . Em outras palavras, um fluxo axissimétrico é menos "confinado" ou "restrito" do que um fluxo bidimensional correspondente. Portanto, poderíamos ter esperado o comportamento oposto.
Comparamos nosso coeficiente de arrasto previsto com o do experimento . A discrepância é de apenas cerca de - concordância muito melhor do que no caso bidimensional. As razões para essa melhoria não são claras. Os fluxos axissimétricos tendem a ser menos instáveis e os vórtices que eles lançam são geralmente menos coerentes e mais fracos. Isso pode contribuir para algumas das melhorias. Pode ser meramente fortuito que o modelo de turbulência produza melhores resultados para o caso axissimétrico em comparação com o caso .
É isso, galera. Bora pra praticar mais pra ficar craque.
Resposta
