Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 156

Considere o diagrama do Problema 4.154. Se m = 100   k g , ρ = 1000   k g / m 3 e A = 0,01   m 2 , determine a velocidade V do jato requerida para que o carrinho seja levado ao repouso depois de um segundo se a velocidade inicial do carrinho for u 0 = 5   m / s . Para esta condição, trace um gráfico da velocidade u e da posição x do carrinho como funções do tempo. Qual é o máximo valor de x , e quanto tempo o carrinho leva para retornar à sua posição inicial?

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V = v + u ) ;
  4. Escoamento uniforme.
  5. Força de resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A

- ∫ V C a r ρ d ∀ = ∫ S C V ( ρ V ) d A

- a r ⋅ m = u 1 - ρ v + u A + u 2 ⋅ m ˙ 2 + u 3 ⋅ m ˙ 3

Sendo:

a r = d u d t ;

u 1 = - ( v + u ) ;

u 2 = u 3 = 0 .

Temos:

- d u d t ⋅ m = ρ v + u 2 A

Separando os termos:

∫ u 0 u 1 v + u 2 d v + u = - ∫ 0 t ρ A m d t

Integrando, temos:

- 1 v + u + 1 v + u 0 = - ρ A t m

1 v + u = 1 v + u 0 + ρ A t m

v + u = 1 1 v + u 0 + ρ A t m

u = - v + 1 1 v + u 0 + ρ A t m

Passo 3

Calculando v .

Sendo:

t = 1 s ;

u = 0 ;

ρ = 1000   k g / m 3 ;

A = 0,01   m 2 ;

u 0 = 5   m / s ;

m = 100   k g .

Temos

0 = - v + 1 1 v + 5 + 1000 ⋅ 0,01 100 ⋅ 1

v = 1 1 v + 5 + 0,1

v 1 v + 5 + 0,1 = 1

v 1 + 0,1 v + 0,5 v + 5 = 1

v + 0,1 v 2 + 0,5 v = v + 5

0,1 v 2 + 0,5 v - 5 = 0

v = 5   m / s

Passo 4

Temos que:

d x d t = u = - v + 1 1 v + u 0 + ρ A t m

Separando os termos:

d x = - v + 1 1 v + u 0 + ρ A t m d t

Integrando:

x = - v t + m ρ A ln ⁡ 1 + ρ A v + u 0 m t

Passo 5

Qual é o máximo valor de x ?

x é máximo quando u = 0 , e isso ocorre em t = 1   s como nos foi falado no enunciado.

Então:

x = - 5 ⋅ 1 + 100 1000 ⋅ 0,01 ln ⁡ 1 + 1000 ⋅ 0,01 ⋅ 5 + 5 100 ⋅ 1 = 1,93   m

Quanto tempo o carrinho leva para retornar à sua posição inicial?

Nesse caso, x = 0 .

Então:

0 = - 5 ⋅ t + 100 1000 ⋅ 0,01 ln ⁡ 1 + 1000 ⋅ 0,01 ⋅ 5 + 5 100 ⋅ t

5 t = 10 ln ⁡ 1 + t

t ln ⁡ 1 + t = 2

t = 2,51   s

Passo 6

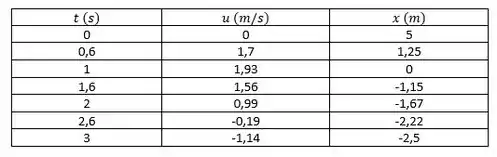
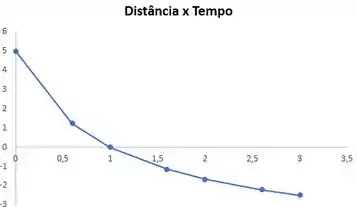
Traçando um gráfico da velocidade u e da posição x do carrinho como funções do tempo:

Resposta

x = 1,93   m

t = 2,51   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um líquido incompressível de viscosidade desprezível é bombeado com uma vazão volumétrica total Q através de dois pequenos orifícios para dentro de uma pequena fresta entre discos paralelos estreitame
Projete uma clepsidra (relógio de água Egípcio) – um recipiente do qual água é drenada por gravidade através de um orifício no fundo e que indica o tempo pelo nível da água remanescente. Especifique a
Um líquido cai verticalmente dentro de um canal retangular aberto, curto e horizontal, de largura b . A vazão volumétrica total, Q , é uniformemente distribuída sobre a área b L . Despreze efeitos vis
Um disco de massa m é restringido horizontalmente, mas está livre para movimentar na vertical. Um jato de água atinge o disco por baixo. O jato sai do bocal com velocidade inicial V 0 . Obtenha uma eq
Um modelo de foguete, a propelente sólido, tem uma massa de 69,6g , da qual 12 ,5g são de combustível. O foguete produz 5,75N de empuxo por um período de 1,7s . Para essas condições, calcule a velocid