Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 73
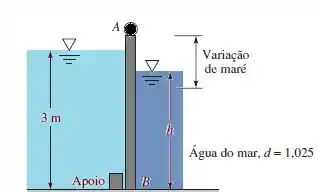
A comporta AB tem 1,5 m de largura e abre para permitir a saída de água doce quando a maré do oceano estiver abaixando. A articulação em A está 0,6 m acima do nível de água doce. Em qual nível h do oceano a comporta abrirá? Despreze o peso da comporta.
Passo 1
A primeira coisa que precisamos entender aqui é que se você se ligar, vamos ter duas forças hidrostáticas atuando sobre a comporta AB, certo? Mas elas terão altura de atuação, , diferentes porque possuem alturas de coluna de fluido diferentes, beleza?
Vamos então começar calculando a força hidrostática do lado da água doce, que aqui eu vou colocar o subíndice e “ad”.
Para uma placa plana, o centroide dela será na metade do seu comprimento, logo .
Assim, temos:
Passo 2
Agora vamos calcular a força hidrostática do lado da água do mar, mas antes vamos passar já a densidade relativa para absoluta!!!
Então podemos calcular a força hidrostática que atua na comporta, lembrando que a altura utilizada na fórmula abaixo é metade da altura da placa que está submersa no fluido.
Passo 3
Bem, agora que lá vamos nós olhar para a figura novamente!!!
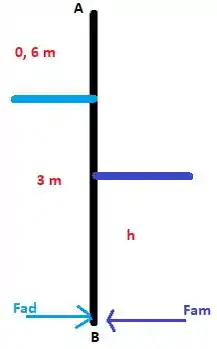
A gente então percebe que se formos calcular os momentos em torno do ponto B, vamos precisar saber a distância que as forças estão atuando em seus centros de pressão.
A gente pode ir por um caminho mais fácil aqui ao invés de precisar resolver a equação de . Sabemos que para uma placa plana, seu centro de pressão equivale a 1/3 do seu comprimento submerso. Então você vai concordar comigo que, olhando para o desenho acima, a altura que a força do lado da água salgada tem distância de (3+0,6 – h/3).
Para a água doce, temos qual distância de A até o centro de pressão? Bem, a altura total é de 3,6 m, beleza? Mas como vimos, o centro de pressão deve estar a 1/3 do comprimento submerso da placa, ou seja, se 3 metros de placa estão submersos, 1/3 x 3 = 1m.
Logo,
Passo 4
Feito isso, podemos escrever nosso somatório de momento em torno de B:
Resolvendo para temos que: