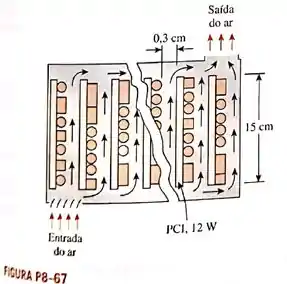
Um computador resfriado por ventilação contém oito placas de circuito impresso (PCI), cada uma dissipando de potência. As placas têm de altura e de comprimento. A folga entre as pontas dos componentes da placa e a superfície traseira da outra placa adjacente é . O ar de resfriamento é fornecido por um ventilador de montado na entrada. Se o aumento da temperatura do ar ao escoar através do computador não exceder , determine a vazão de ar que o ventilador deve fornecer, a fração do aumento de temperatura do ar que é devido ao calor gerado pelo ventilador e seu motor e a temperatura mais alta admissível do ar na entrada, se a temperatura da superfície dos componentes não exceder em qualquer parte do sistema. Use as propriedades do ar a .

a) Podemos calcular a vazão mássica usando a formula para a taxa de transferência de calor. Assim temos:

Onde é a taxa de transferência de calor total. Ou seja, a soma de cada circuito mais o ventilador.

Substituindo os termos pelos dados fornecidos no enunciado, temos:

Portanto, a vazão mássica é .

b) Temos que a energia usada pelo ventilador, pode ser expressa da seguinte forma:

Podemos isolar a diferença de temperaturas da seguinte forma:

Substituindo os termos pelos dados fornecidos no enunciado, temos:

Assim, a fração do aumento de temperatura do ar que é devido ao calor gerado pelo ventilador e seu motor pode ser dado da seguinte forma:

Substituindo os termos pelos dados fornecidos e calculados, temos:

Portanto, a fração do calor gerado pelo ventilador é .

c) Para determinar a temperatura mais alta admissível do ar na entrada, vamos começar calculando a velocidade média. Assim temos:

Aqui, é a vazão mássica, é a densidade do ar e é a área da seção transversal.

Substituindo os termos pelos dados fornecidos e calculados, temos:

Também precisamos calcuar o diâmetro hidráulico. Podemos fazer isso usando a seguinte relação:

Substituindo os termos pelos dados fornecidos, temos:

Com a velocidade média e o diâmetro hidráulico, podemos calcular o número de Reynolds. Fazemos isso utilizando a seguinte relação:

Aqui, é a viscosidade cinemática. Substituindo os termos pelos dados fornecidos e calculados, temos:

Como o número de Reynolds é menor que , o fluxo é laminar.

Assim, o comprimento da entrada é dado da seguinte forma:

Substituindo os termos pelos dados fornecidos e calculados, temos:

Esse comprimento é menor que o comprimento total; portanto, o fluxo é um fluxo laminar totalmente desenvolvido. Agora, calculamos a o valor , onde, é a atura das placas e é a folga entre as placas. Assim temos:

Na tabela “Números de Nusselt para diferentes seções transversais”, o número de Nusselt para  é encontrado como .

Podemos calcular o coeficiente de transferência de calor usando a relação do número de Nusselt. Assim temos:

Aqui  é a condutividade térmica. Substituindo os termos pelos dados encontrados anteriormente, temos:

Como sabemos que a temperatura mais alta estará no ponto de saída, podemos calcula-la usando a equação para transferência de calor. Assim temos:

Aqui, é a transferência de calor total, é a área da superfície, é a temperatura na superfície, é a temperatura na saída. Substituindo os termos pelos dados encontrados anteriormente, temos:

Portanto, a temperatura de saída é .

Podemos encontrar a temperatura na entrada usando a relação dada no enunciado. Temos que:

Portanto, a temperatura de entrada é .