Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 125

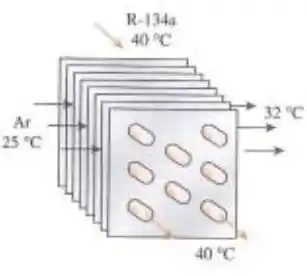
O condensador do ar-condicionador de uma sala é projetado para rejeitar calor a uma taxa de 22500 k J h do refrigerante 134a, quando o fluido refrigerante é condensado a uma temperatura de 40°C. O ar c p = 1005 J k g K escoa sobre a serpentina aletada do condensador, entra 25°C e o deixa a 32°C. Se o coeficiente global de transferência de calor baseado no lado do refrigerante é 150 W m 2 K , determine a área de transferência de calor no lado do refrigerante.

Passo 1

Bora começar mais uma??

Bom, nós queremos a área superficial para uma dada taxa de transferência de calor, certo?

Nós sabemos que:

Q ˙ = U F A s ∆ T l m

Já sabemos que:

Q ˙ = 22500 k J h × 1 h 3600   s = 6,25 k J s = 6,25   k W

U = 1 5 0 W m 2 . K = 0 , 150 k W m 2 . K

Como estamos falando do condensador:

F = 1

Passo 2

Beleza galera, agora só precisamos calcular a diferença média logarítima:

∆ T l m = ∆ T 1 - ∆ T 2 ln ⁡ ∆ T 1 ∆ T 2

Se:

∆ T 1 = T q ,   e n t r a - T f ,   s a i

∆ T 2 = T q ,   s a i - T f ,   e n t r a

Lembrando que:

T q ,   e n t r a = T q ,   s a i = 4 0 ° C

T f ,   e n t r a = 2 5 ° C

T f ,   s a i = 32 ° C

Então:

∆ T 1 = 4 0 ° C - 3 2 ° C = 8 ° C

∆ T 2 = 4 0 ° C - 2 5 ° C = 15 ° C

Agora podemos calcular a diferença média logarítima:

∆ T l m = 8 ° C - 15 ° C ln ⁡ 8 ° C 15 ° C

∆ T l m = 11,13 ° C

Com tudo isso nós já conseguimos calcular a área:

6,25   k W = 1 0,15 k W m 2 K A s 11,13 ° C

A s = 3,74   m ²

Toop, né ?!

Resposta

3,74   m ²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trocador de calor com 2 passes no casco e 4 passes no tubo é usado para aquecimento de hidrocarboneto c p = 2,0 k J k g K permanentemente de 20°C para 50°C. Água entra no lado do casco a 80°C e o d
Em um trocador de calor líquido-líquido de escoamento paralelo, as temperaturas de entrada e saída do fluido quente são 150 ℃ ℃ e 90 ℃ ℃, enquanto as do fluido frio são 30 ℃ ℃ e 70 ℃ ℃, respectivament
36 - Quando as temperaturas de saída dos fluidos em um trocador de calor não são conhecidas, ainda é prático usar o método LMTD?Explique.
33 - A temperatura de saída do fluido frio em um trocador de calor pode ser superior que a temperatura de saída do fluido quente em um trocador de calor de escoamento paralelo?E em um trocador de calo
32 - A diferença entre as temperaturas dos fluidos quente e frio em um trocador de calor é dada como Δ T 1 em uma extremidade e Δ T 2 na outra extremidade.A diferença de temperatura média logarítmicaΔ