Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 11.Problemas - Ex. 129

Um trocador de calor com 2 passes no casco e 4 passes no tubo é usado para aquecimento de hidrocarboneto c p = 2,0 k J k g K permanentemente de 20°C para 50°C. Água entra no lado do casco a 80°C e o deixa a 40°C. há 160 tubos de parede fina, cada um com um diâmetro de 2,0 cm e comprimento de 1,5 m. Os coeficientes de transferência de calor do lado do tubo e do lado do casco são 1,6   e   2,5 k W m 2 K , respectivamente. Calcule:

  1. A taxa de transferência de calor e as vazões mássicas das correntes da água e do hidrocarboneto;
  2. A temperatura de saída do hidrocarboneto com redução de 5°C, devido à deposição de sólidos na superfície do tubo. Estime a magnitude do fator de incrustação.

Passo 1

Bora continuar !!

Para calcular a taxa de transferência de calor nós vamos usar a fórmula:

Q ˙ = U F A s ∆ T l m

Lembrando que:

A s = n π D L

Então:

Q ˙ = U F n π D L ∆ T l m

O que nós sabemos ?

D = 2   c m = 0,02   m

L = 1,5   m

n = 10 0   t u b o s

Bom, nós não temos nada sobre F ,   U e ∆ T l m , então vamos a lutaa !!!

Passo 2

Se a espessura da parede é insignificante, o coeficiente vai ser calculado em relação ao fluido frio e quente:

U = 1 1 h q + 1 h f

Já sabemos que:

h q = 2,5 k W m 2 K

h f = 1,6   k W m 2 K

Substituindo:

U = 1 1 2,5 k W m 2 K + 1 1,6   k W m 2 K

U = 0,975   k W m 2 K

Passo 3

Beleza galera, agora nós precisamos calcular a diferença média logarítima:

∆ T l m = ∆ T 1 - ∆ T 2 ln ⁡ ∆ T 1 ∆ T 2

Se:

∆ T 1 = T q ,   e n t r a - T f ,   s a i

∆ T 2 = T q ,   s a i - T f ,   e n t r a

Lembrando que:

T q ,   e n t r a = 8 0 ° C

T q ,   s a i = 4 0 ° C

T f ,   e n t r a = 2 0 ° C

T f ,   s a i = 50 ° C

Então:

∆ T 1 = 8 0 ° C - 5 0 ° C = 3 0 ° C

∆ T 2 = 40 ° C - 2 0 ° C = 2 0 ° C

Agora podemos calcular a diferença média logarítima:

∆ T l m = 30 ° C - 20 ° C ln ⁡ 30 ° C 20 ° C

∆ T l m = 24,66 ° C

Passo 4

Agora precisamos do fator de correção:

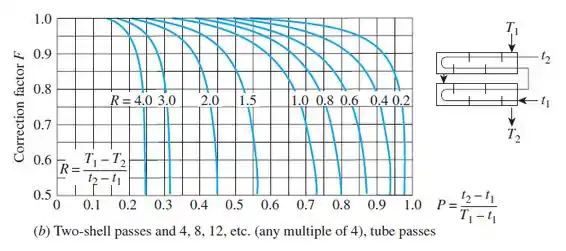
Vamos começar calculando R e P:

R = T q ,   e n t r a - T q ,   s a i T f ,   s a i - T f ,   e n t r a = 80 ° C - 40 ° C 50 ° C - 20 ° C = 1,3

P = T f ,   s a i - T f ,   e n t r a T q ,   e n t r a - T f ,   e n t r a = 50 ° C - 20 ° C 80 ° C - 20 ° C = 0,5

Então:

F ≅ 0,91

Colocando a fórmula do Passo 1:

Q ˙ = 0,975   k W m 2 K 0,9 1 π × 160 × 0,02   m × 1,5   m 24,66 ° C

Q ˙ = 329,9   k W

Passo 5

Para achar as vazões mássicas nós vamos usar o calor com as temperaturas para calcular as vazões mássicas, começando pela água:

Q ˙ = m q ˙ c p , q T q ,   e n t r a - T q ,   s a i

Se:

c p , q = 4,18 k J k g . K

Substituindo:

329,9   k W = m q ˙ 4,18 k J k g . K 80 ° C - 4 0 ° C

m á g u a ˙ = 1,973 k g s

Para o hidrocarboneto:

Q ˙ = m f ˙ c p , f T f ,   s a i - T f ,   e n t r a

Se:

c p , f = 2 k J k g . K

Substituindo:

329,9   k W = m q ˙ 2 k J k g . K 5 0 ° C - 2 0 ° C

m h i d r o c a r b o n e t o ˙ = 5,498 k g s

Terminamos a letra (a), mas ainda vamos para a (b) !!

Passo 6

Bom galera, na letra (b) temos a temperatura de saída do hidrocarboneto com redução de 5°C, devido à deposição de sólidos na superfície do tubo. Então:

T q ,   e n t r a = 80 ° C

T f ,   e n t r a = 20 ° C

T f ,   s a i = 4 5 ° C

Agora a nova taxa de transferência de calor:

Q n o v a ˙ = m f ˙ c p , f T f ,   s a i - T f ,   e n t r a

Substituindo:

Q n o v a ˙ = 5,498 k g s 2 k J k g . K 4 5 ° C - 20 ° C

Q n o v a ˙ = 274,9   k W

Com esta taxa de transferência de calor nós poderemos calcular a nova temperatura de saída do fluido quente.

Como? Usando a mesma fórmula, ok?

Q n o v a ˙ = m q ˙ c p , q T q ,   e n t r a - T q ,   s a i

Substituindo:

274,9   k W = 1,973 8 k g s 4,18 k J k g . K 80 ° C - T q ,   s a i

T q ,   s a i = 46,66 ° C

Com as novas temperaturas nós vamos calcular a nova diferença média logarítima:

∆ T 1 = 80 ° C - 4 5 ° C = 3 5 ° C

∆ T 2 = 46,66 ° C - 20 ° C = 2 6,66 ° C

Na fórmula:

∆ T l m = 35 ° C - 26,66 ° C ln ⁡ 35 ° C 26,66 ° C

∆ T l m = 30,641 ° C

Mas ainda falta o fator de correção!!

Passo 7

Para isso nós vamos usar a mesma figura do Passo 4, ok?

Calculando R e P:

R = T q ,   e n t r a - T q ,   s a i T f ,   s a i - T f ,   e n t r a = 80 ° C - 46,66 ° C 4 5 ° C - 20 ° C = 1,3

P = T f ,   s a i - T f ,   e n t r a T q ,   e n t r a - T f ,   e n t r a = 4 5 ° C - 20 ° C 80 ° C - 20 ° C = 0 , 4

Então:

F ≅ 0,97

Com estes novos dados nós vamos achar um novo coeficiente global de transferência de calor, ok?

Colocando na fórmula do Passo 1:

274,9   k W = U n o v a 0,97 π × 160 × 0,02   m × 1,5   m 30,641 ° C

U n o v a = 0,6133 k W m 2 . K

Passo 8

Agora, este novo coeficiente global levara em conta o coeficiente antigo e a resistência devido à incrustação:

1 U n o v a = 1 U a n t i g a + R f

Reorganizando:

R f = 1 U n o v a - 1 U a n t i g a

Substituindo:

R f = 1 0,6133 k W m 2 . K - 1 0,975   k W m 2 K

R f = 0,6049 m 2 . K k W

Ufaaaa !!

Foi grande, mas acabou !!

Resposta

  1. Q ˙ = 329,9   k W         m á g u a ˙ = 1,973 k g s         m h i d r o c a r b o n e t o ˙ = 5,498 k g s ;
  2. R f = 0,6049 m 2 . K k W .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ar ( c p = 1005J / k g ⋅ K ) deve ser preaquecido por gases quentes em um trocador de calor de escoamento cruzado antes de entrar em um forno. O ar entra no trocador de calor a 95 kPa e 20 °C, a uma t
Repita o Prob. 11-58 para uma vazão mássica de água de 3 kg/s.
Óleo de motor ( c p = 2100J / k g ⋅ K ) deve ser aquecido de 20 °C para 60 °C a uma taxa de 0,3 kg/s em um tubo de cobre de parede fina com diâmetro de 2 cm pela condensação externa de vapor a uma tem
Um trocador de calor de único passe deve ser projetado para aquecer 45000 kg de água em uma hora a partir de 15 °C para 40 °C por condensação de vapor de água a 110 °C no lado do casco. Cada tubo tem
Em uma fábrica têxtil, águas residuais de tingimento ( c p = 4295J / k g ⋅ K ) a 80 °C devem ser utilizadas para preaquecimento de água fresca ( c p = 4180J / k g ⋅ K ) a 10 °C com a mesma vazão em um