Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 96

O fator U global de uma janela fixa com vidros duplos e quadro de madeira é dado pelo fabricante como sendo U = 2,76   W / m 2 · K nas condições de ar interior estacionário e ventos externos de 12   k m / h . Qual seria o fator U se a velocidade do vento externo fosse duplicada?

Passo 1

Dados fornecidos:

Coeficiente geral de transferência de calor: U = 2,76   W / m 2 ⋅ K

Velocidade do ar exterior: V = 12   k m / h  

Velocidade do ar exterior duplicada: V ' = 2 V = 24   k m / h

Coeficiente geral de transferência de calor para V ' : U ' = ?

Propriedades:

Os coeficientes de transferência de calor na superfície exterior da janela são  h o = 22,7   W / m 2 ⋅ K durante ventos de 12   k m / h e h ' o = 34,0   W / m 2 ⋅ K   durante ventos de 24   k m / h (do livro).

Premissas:

(1) As propriedades térmicas das janelas são constantes.

(2) Coeficientes de transferência de calor são constantes.

Passo 2

Podemos fazer o seguinte esquema mostrando a janela de painel duplo:

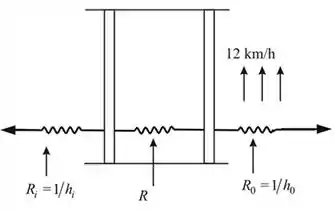
Passo 3

Primeiro, vamos começar calculando as resistências de convecção correspondentes para as duas velocidades na superfície externa da janela. Podemos obter com a seguinte relação:

R o = 1 h o

Para o vento com velocidade de 12   k m / h e coeficiente de transferência térmica externa h o = 22,7   W / m 2 ⋅ K , a resistência correspondente é:

R o = 1 h o = 1 22,7   W / m 2 ⋅ K = 0,0440 5   m 2 ⋅ K / W

Para o vento com velocidade de 24   k m / h e coeficiente de transferência térmica externa h o = 34,0   W / m 2 ⋅ K , a resistência correspondente é:

R ' o = 1 h ' o = 1 34,0   W / m 2 ⋅ K = 0,02941   m 2 ⋅ K / W

Passo 4

Podemos calcular a resistência geral usando a seguinte expressão:

R = 1 U

Substituindo os termos da equação acima pelos dados fornecidos, temos:

R = 1 2,76   W / m 2 ⋅ K = 0,3623   m 2 ⋅ K / W

Passo 5

Agora, para uma velocidade de vento de 12   k m / h , a resistência geral é pode ser escrita da seguinte forma:

R = R i + R e s p a ç o + R o

Substituindo os termos da equação acima pelos dados calculados, temos:

0,3623   m 2 ⋅ K / W = R i + R e s p a ç o + 0,0440 5   m 2 ⋅ K / W

R i + R e s p a ç o = 0,3623   m 2 ⋅ K / W - 0,0440 5   m 2 ⋅ K / W

R i + R e s p a ç o = 0,3183   m 2 ⋅ K / W

Passo 6

Agora, para uma velocidade de vento de 24   k m / h , a resistência geral é pode ser escrita da seguinte forma:

R ' = R i + R e s p a ç o + R ' o

Aqui, R i e R e s p a ç o são os mesmos que para o vento de 12   k m / h , pois não teve alteração. Assim, substituindo os termos da equação acima pelos dados calculados, temos:

R ' = 0,3183   m 2 ⋅ K / W + 0,02941   m 2 ⋅ K / W

R ' = 0,3477   m 2 ⋅ K / W

Passo 7

Assim, temos que o coeficiente geral de transferência de calor na velocidade do vento de 24   k m / h é;

U ' = 1 R '

Substituindo os termos da equação acima pelos dados calculados, temos:

U ' = 1 0,3477   m 2 ⋅ K / W = 2,88   W / m 2 ⋅ K

Portanto, se a velocidade do vento externo for dobrada, o coeficiente geral de transferência de calor será  2,88   W / m 2 ⋅ K .

Resposta

U ' = 2,88   W / m 2 ⋅ K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma seção horizontal de um teto plano, que tem as mesmas dimensões de uma seção vertical de uma parede. Para ambas as seções, as superfícies expostas ao espaço preenchido pelo ar estão a 18°
A placa absorvedora e a placa de cobertura adjacente em um coletor solar plano estão a 70° e 35°C, respectivamente, e encontram-se separadas por uma camada de ar com 0,05 m de espessura. Qual é a taxa
Considere um sistema de armazenamento térmico no qual o material que muda de fase (parafina) é confinado em um grande reservatório, cuja superfície inferior, horizontal, é mantida a Ts = 50°C por água
Uma cavidade retangular é formada por duas placas paralelas quadradas com 0,5 m de lado, separadas por uma distância de 50 mm. As fronteiras laterais da região entre as placas são isoladas. A placa aq
Uma chapa fina de vidro de uma janela com 1m de lado separa o ar quiescente de uma sala a T ∞ , i=20 ° C do ar ambiente externo, também quiescente, a T ∞ , e=220 ° C . As paredes da sala e a vizinhanç