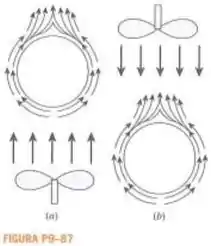
Um cilindro com diâmetro de horizontal tem sua temperatura de superfície mantida a . Água a está fluindo através do cilindro a uma velocidade de . Determine o número de Nusselt, considerando que a água esteja fluindo (a) para cima e (b) para baixo.

Para resolver essa questão, podemos começar calculando a temperatura do filme. Assim temos:

Aqui,  é a temperatura da superfície da haste e  é a temperatura da água.

Com a temperatura de filme, podemos obter as propriedades da água na tabela A-9. Assim temos:

Coeficiente de expansão volumétrico:

Viscosidade dinâmica:

Densidade:

Número Prandtl:

Com os dados obtidos nos passos anteriores, vamos calcular o Número de Reynolds usando a seguinte relação:

Aqui,  é a velocidade da água,  é o diâmetro da haste, é a densidade da água e é a viscosidade dinâmica. Substituindo os termos da equação pelos dados obtidos, temos:

Vamos precisar calcular também o Número Grashof usando a seguinte relação:

Aqui,  é aceleração devido à gravidade, é a temperatura da superfície,  é a temperatura da água e  é comprimento característico. Para cilindro horizontal, o comprimento da característica é igual ao diâmetro da barra. Substituindo os termos da equação pelos dados obtidos, temos:

No livro, podemos encontrar que a convecção natural é desprezível se a razão entre o número de Grashof e o quadrado do número de Reynolds for menor que .

Assim vamos calcular essa relação para ver se os efeitos de convecção natural são importantes para a transferência de calor no processo. Assim temos:

A partir do valor da razão, fica entre e , as convecções forçadas e naturais são significativas.

Agora, podemos calcular o número de Nusselt para convecção forçada da seguinte forma:

Substituindo os termos da relação acima pelos dados calculados e coletados, temos:

Agora, vamos calcular o número de Rayleigh usando a seguinte relação:

Substituindo os termos da equação pelos dados obtidos, temos:

Com o número de Rayleigh, podemos encontrar o número de Nusselt para convecção natural em cilindro horizontal. Assim temos:

Substituindo os termos da equação pelos dados calculados anteriormente, temos:

a) Podemos desenhar um diagrama esquemático quando o fluxo de vapor estiver para cima.

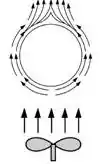
Podemos calcular o número de Nusselt quando o fluxo estiver para cima da seguinte maneira:

Substituindo os termos da equação pelos dados obtidos, temos:

Portanto, o número de Nusselt combinado para fluxo ascendente é .

b) Podemos desenhar um diagrama esquemático quando o fluxo de vapor estiver para baixo.

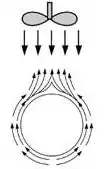
Podemos calcular o número de Nusselt quando o fluxo estiver para baixo da seguinte maneira:

Substituindo os termos da equação pelos dados obtidos, temos:

Portanto, o número combinado de Nusselt para o fluxo da ala inferior é .