Uma corrente elétrica passa através de um condutor horizontal, com de diâmetro e emissividade de , quando este condutor se encontra imerso em água à pressão atmosférica.
(a) Estime a dissipação de potência por unidade de comprimento do condutor necessária para manter sua temperatura superficial em .
(b) Para diâmetros do condutor iguais a e , calcule e represente graficamente a dissipação de potência por unidade de comprimento como uma função da temperatura superficial para . Em uma figura separada, represente a contribuição percentual da radiação como uma função de .
Passo 1
Vamos lá! Nosso problema pede a potência necessária para manter a temperatura superficial proposta, mas antes não vamos esquecer do nosso velho esboço pra facilitar nosso problema.
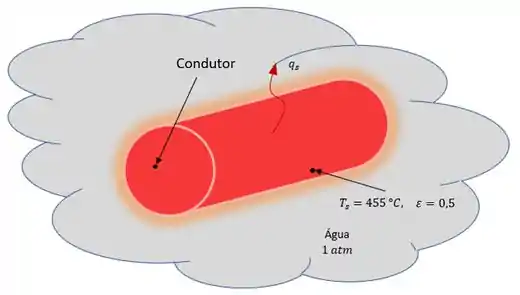
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
a)
Vamos lá! Iremos usar os dados da tabela para água liquida saturada a e da tabela para vapor d’água, assim temos que a transferência total de calor em função do comprimento é dada por:
, assim de acordo com a figura para um grande assim a ebulição em filme em piscina vai acontecer, assim temos da equação .
Ou
Estimando o coeficiente convectivo a partir da equação , temos:
Isolando , temos:
Calculando agora , temos:
Assim temos que
Por fim, podemos calcular a taxa de transferência de calor que apresentamos antes:
Passo 3
b)
Se fizermos o mesmo processo da letra (a) variando a espessura do fio e a temperatura de superfície desejada chegamos ao seguinte gráfico (recomendo o uso de software para realizar isso pois fazer ponto a ponto é exaustivo):
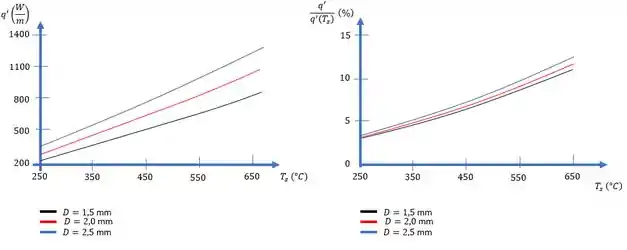
Isso é tudo pessoal! \o/

Resposta
a)