Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 112
Muitas das superfícies sólidas nas quais os valores dos coeficientes de acomodação térmica e de momento foram medidos são muito diferentes das usadas em micro e nanodispositivos. Represente graficamente o número de Nusselt associado ao escoamento laminar plenamente desenvolvido, com fluxo na superfície constante, versus o diâmetro do tubo para 1 μm ≤ D ≤ 1 mm e (i) = 1, = 1, (ii) = 0,1, = 0,1, (iii) = 1, = 0,1, (iv) = 0,1, = 1. Para tubos com quais diâmetros os coeficientes de acomodação começam a influenciar a transferência de calor convectiva? Para qual combinação de e o número de Nusselt exibe a menor sensibilidade em relação a mudanças no diâmetro do tubo? Qual combinação resulta em números de Nusselt maiores do que o valor convencional para o escoamento laminar plenamente desenvolvido com fluxo na parede constante, = 4,36? Qual combinação está associada aos menores valores do número de Nusselt? O que você pode falar sobre a capacidade de se prever coeficientes de transferência de calor por convecção, em dispositivos de pequena escala, se os coeficientes de acomodação não forem conhecidos para o material com o qual o dispositivo é fabricado? Use propriedades do ar na pressão atmosférica e a T = 300 K.
Passo 1
Beleza! Vamos começar o exercício pegando as propriedades do ar na pressão atmosférica a uma temperatura de 300 K. Para isso, vamos recorrer a tabela A.4 do apêndice A, onde conseguimos as seguintes propriedades:
Agora, nós vamos recorrer à figura 2.8 vista no capítulo 2, onde poderemos pegar os valores dos diâmetros moleculares, então temos:
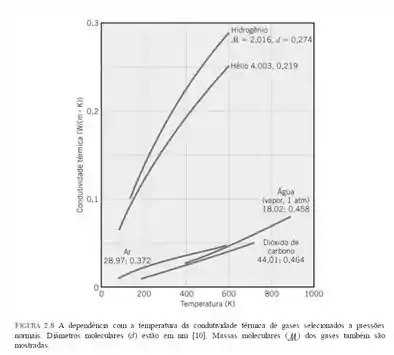
Com ela, podemos ver que o diâmetro molecular do ar será:
Agora, sabemos também que a constante de gás ideal para o ar é dada por:
Então, com isso, podemos calcular o calor específico a volume constante, onde teremos:
E, agora podemos calcular a razão entre os calores específicos, dado por:
Passo 2
Agora nós vamos recorrer à equação do livre percurso médio, dado pela equação 2.11, onde temos:
Sabendo que a constante de Boltzmann é dada por , então, substituindo os valores conhecidos nessa equação, teremos:
Agora, nós podemos encontrar o número de Nusselt através da equação 8.78a:
Onde temos dado por:
E que é dado por:
E, por sua vez, é dado por:
Passo 3
Com isso, juntando as equações do passo 2, substituindo uma na outra e por fim, jogando todas elas na equação para Nusselt, podemos substituir os valores de e para os diferentes casos, fazendo isso, chegamos nas seguintes relações para o número de Nusselt e o diâmetro da tubulação:
Passo 4
Agora vamos pra análise do gráfico do passo 3. Os coeficientes de acomodação começam a influenciar a transferência de calor convectiva para diâmetros de até 300-500 .
A menor sensibilidade do número de Nusselt em relação aos números de .
A combinação que resulta em um número de Nusselt maior que 4,36 ocorre para e e para diâmetros menores que .
O menores valores do número de Nusselt estão associados para e .
Os coeficientes de transferência de calor por convecção podem ser determinados com base em e principalmente para tubulações de pequenos diâmetros.
Resposta
Ei, a resposta está no passo a passo :)