Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 23
Um equipamento experimental para simular o núcleo de um reator nuclear é constituído por um longo tubo metálico com paredes delgadas, diâmetro D e comprimento L, que é aquecido eletricamente para produzir uma distribuição senoidal de fluxo térmico:
sendo x a distância medida da entrada do tubo. Um fluido, a uma temperatura de entrada , escoa através do tubo a uma vazão . Admitindo que o escoamento seja turbulento e esteja plenamente desenvolvido ao longo de todo o comprimento do tubo, desenvolva expressões para:
- a taxa total de transferência de calor, q, do tubo para o fluido;
- a temperatura de saída do fluido, ;
- a distribuição axial das temperaturas na parede, ;
- a magnitude e a posição da temperatura mais elevada na parede do tubo;
- Considere um tubo com 40 mm de diâmetro e 4 m de comprimento, com uma distribuição senoidal de fluxo térmico para a qual . O fluido escoando no tubo tem uma vazão mássica de , um calor específico de , uma temperatura na entrada de 25°C e um coeficiente de transferência de calor de . Represente graficamente as temperaturas média do fluido e superficial como funções da distância ao longo do tubo. Identifique características importantes dessas distribuições. Explore os efeitos de variações de ± 25% no coeficiente de transferência de calor e no fluxo térmico sobre essas distribuições.
Passo 1
Faaaaaaaaaaaaalaa galerinha!!
Bora continuar?!
Na letra (a) nós queremos achar a taxa total de transferência de calor, q, do tubo para o fluido!
De uma coisa nós sabemos:
Substituindo :
A letra (a) está OK!!
Passo 2
A letra (b) nos pede a temperatura de saída do fluido,
E para isso vamos usar outra relação bem conhecida:
Isolamos o que queremos:
Como o q nós já sabemos:
Animados para a (c)?!
Passo 3
Vamos achar agora a distribuição axial das temperaturas na parede,
Podemos usar a relação:
Isolando
Igualando as equações para o calor dadas no Passo 1 e 2:
E substituindo
Substituindo na relação dada para
Passo 4
Agora vamos para a letra (d)!!
Aqui nós queremos a magnitude e a posição da temperatura mais elevada na parede do tubo!
A temperatura máxima é obtida quando:
Derivando:
Então a temperatura máxima ocorre quando o x assume este valor !!
Passo 5
E finalizamos com a letra (e) !!
Sabendo que:
Lembrando que:
Variando x:
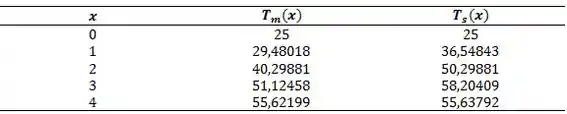
Colocando nossos resultados no gráfico:
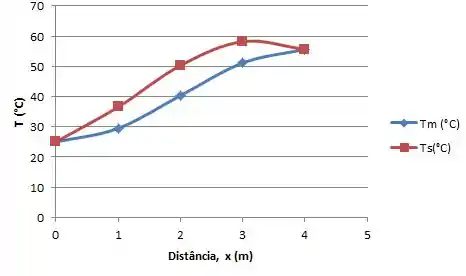
Mas ainda não acabamos, devemos observar os efeitos que ocorrem quando variamos o coeficiente convectivo em ± 25%.
Quando o coeficiente aumenta 25%,
No gráfico:
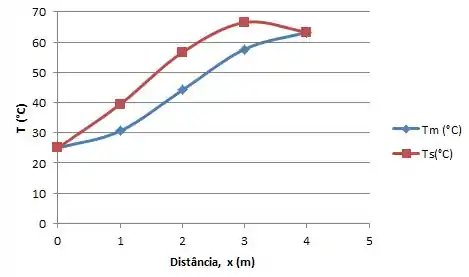
E quando diminuímos 25%,
E seu gráfico:
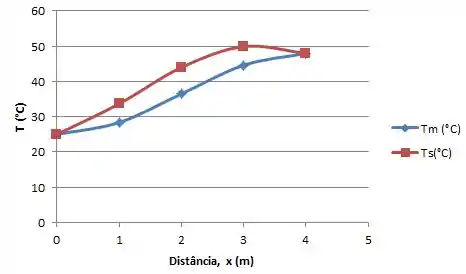
E terminamos mais uma !