Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 1.Problemas - Ex. 82
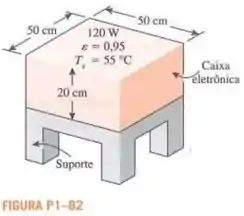
Considere uma caixa eletrônica selada de de altura, com área da base de , colocada em uma câmara de vácuo. A emissividade da superfície externa da caixa é de . Os componentes eletrônicos na caixa dissipam o total de de potência e a temperatura da superfície externa da caixa não pode exceder . Determine a temperatura na qual as superfícies ao redor devem ser mantidas se a caixa for resfriada apenas por radiação. Assuma que a transferência de calor da superfície inferior da caixa para o suporte seja insignificante.
Passo 1
Dados fornecidos:
Altura da Caixa:
Área da base:
Emissividade da superfície:
Potência dissipada:
Temperatura da superfície externa:
Constante de Stefan Boltzmann:
Premissas:
1) Existem condições operacionais estáveis.
2) A transferência de calor por convecção é desconsiderada.
3) A emissividade da caixa é constante e uniforme sobre a superfície exposta.
4) A transferência de calor da superfície inferior da caixa para o suporte é insignificante.
Passo 2
Fala galera!!!
Para resolver essa questão, podemos começar calculando a área da superfície da caixa. Desconsiderando a área de base, a área total de transferência de calor da caixa eletrônica é a seguinte:
Passo 3
Agora, podemos determinar a temperatura ambiente usando a expressão para a transferência de calor por radiação. Assim temos:
Onde é a emissividade, é a constante de Stefan Boltzmann, é a área da superfície, é a temperatura da superfície e é a temperatura do ambiente. Substituindo os termos da equação acima pelos dados fornecidos, temos:
Portanto, a temperatura ambiente deve ser .