Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 34
Considere uma casa com base de e parede de 4m de altura. Todas as quatro paredes da casa têm valores de R de . Duas paredes de não têm janelas. A terceira parede tem cinco janelas de vidro de 0,5 cm de espessura e de tamanho. A quarta parede tem o mesmo tamanho e número de janelas, mas estas são painéis duplos com espaço de ar estagnado de 1,5 cm de espessura, entre duas camadas de vidro de 0,5 cm de espessura. O termostato da casa é fixado em 24 °C, e a temperatura média externa no local é 8 °C durante os 7 meses da temporada de aquecimento. Ignorando qualquer ganho ou perda de radiação direta através das janelas e considerando os coeficientes de transferência de calor nas superfícies interna e externa da casa iguais a 7 e 18 , respectivamente, determine a taxa média de transferência de calor através de cada parede.
Se a casa for aquecida eletricamente e o preço da eletricidade for US$ 0,08/kWh, determine a quantidade de dinheiro que o proprietário da casa poupará por temporada de aquecimento se converter as janelas de painel único em janelas de painel duplo.
Passo 1
Nosso ponto de partida é colocar as hipóteses do nosso problema. São elas que possibilitam a sua solução!
Portanto, temos um problema de transferência de calor em regime permanente, unidimensional e condutividade térmica constante.
Nosso primeiro passo é calcular a taxa de transferência de calor através de cada parede. Começaremos a partir das duas paredes que não tem janela. Utilizando a analogia de circuitos elétricos, podemos associar o seguinte circuito ao caso desta parede:
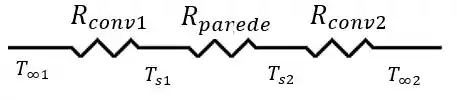
Portanto, calculando os valores das resistências térmicas, temos:
Portanto, a taxa de transferência de calor através dessas paredes é:
E assim determinarmos a quantidade de calor perdido pelas paredes sem janela
Passo 2
Agora, repetiremos os cálculos anteriores para o caso da parede com 5 janelas de vidro simples. Podemos representar elas através do seguinte circuito térmico:
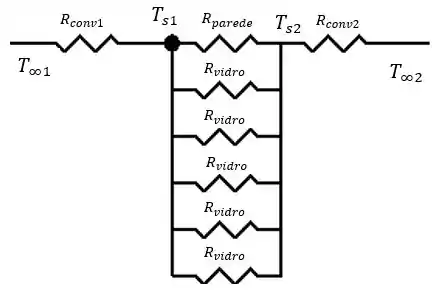
Percebam que temos a associação de resistências em série e resistências em paralelo. Agora, temos uma pegadinha nesta questão. A área das duas paredes é diferente da área das paredes calculadas no Passo 1. Percebam que a casa tem uma base . Portanto, a área das paredes com janela é dada por .
Sendo assim, é necessário recalcularmos as todas as resistências térmicas. Sendo assim,
Agora, para resolvermos o nosso circuito elétrico, vamos começar determinando uma resistência térmica equivalente para as 6 resistências em paralelo. Ele é calculado da seguinte forma:
E com isto resumimos o nosso circuito a três elementos em série . Sendo assim, a taxa de transferência de calor é dada por:
Passo 3
Agora, precisamos calcular a taxa de transferência de calor para a parede com janela de duas camadas. Novamente, o circuito elétrico que corresponde a este caso é dado por:
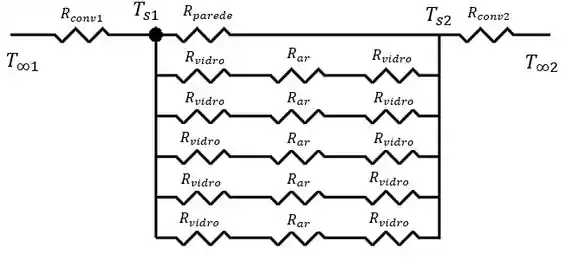
Primeiro, vamos calcular uma resistência térmica equivalente para cada janela . Portanto,
Agora, vamos transformar as resistências em paralelo em 1 resistência equivalente. Portanto,
E com isto resumimos o nosso circuito a três elementos em série . Sendo assim, a taxa de transferência de calor é dada por:
Passo 4
Para finalizarmos, vamos calcular a economia de energia resultante da troca de uma parede com janela simples para uma com dupla camada. Para isto, é necessário calcular a energia economizada ao realizar esta troca. Portanto:
Agora, vamos determinar o preço economizado no período de 7 meses ao evitarmos a perda de 4555,6 W. Sendo assim, temos:
E assim finalizamos a nossa questão!
Resposta
A taxa de transferência de calor para as paredes são:
- Sem janela:
- Com janela simples:
- Com janela de duas camadas:
O valor economizado após a troca das janelas é: