Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 48

Considere a condensação laminar sem ondulações sobre uma placa vertical isotérmica de comprimento L , fornecendo um coeficiente de transferência de calor médio L . Se a placa for dividida em N placas menores, cada uma com comprimento L N   =   L / N , determine uma expressão para a razão entre o coeficiente de transferência de calor médio para todas as N placas e o coeficiente de transferência de calor médio na placa original, h - L , N e h - L ,   1

Passo 1

Vamos lá! Nosso problema pede uma relação entres os coeficientes de transferência de calor para os dois esquemas, mas antes não vamos esquecer do nosso velho esboço pra facilitar nosso problema.

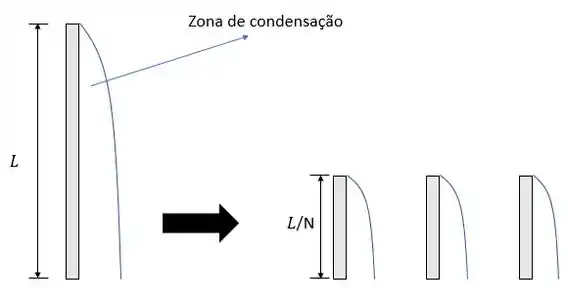
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - P r o p r i e d a d e s   c o n s t a n t e s

Passo 2

Vamos lá, essa é tranquila só precisamos fazer as considerações adequadas, primeiro temos que da equação 10.42 :

P = k l L T s a t - T s u l h f g ' v l 2 g 1 3

Para condensação laminar de forma livre temos da equação 10.43 :

h - L , 1 ∝ P - 1 4 ∝ L - 1 4

Lembrando que o símbolo " ∝ " indica proporcionalidade ou seja h - L , 1 é proporcional a 1 / L 4 .

Da mesma forma para N placas de comprimento L / N temos:

h - L , N ∝ L N - 1 4

Assim fazendo uma correlação entre h - L , N e h - L , 1 temos que:

h - L , N h - L , 1 = N 4

Isso significa que dividir o numero de placas vai reduzir a espessura da zona de condensação em troca de um aumento pequeno no coeficiente de troca de calor, tendo em vista que.

N 4 ≥ 1

Isso é tudo pessoal! \o/

Resposta

h - L , N h - L , 1 = N 4

O coeficiente de calor vai aumentar um pouco divisão de placas.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa vertical de 2m×2m tem um lado exposto a vapor de água saturado a pressão atmosférica e o outro à água de resfriamento que mantém a temperatura da placa a 50 ° C .(a) Qual é a taxa de transfe
Vapor saturado de etilenoglicol a 1 atm está exposto a uma placa vertical, com 300 mm de altura e 100 mm de largura, que se mantém a uma temperatura uniforme de 420 K. Estime a taxa de transferência d
Duas configurações estão sendo analisadas no projeto de um sistema de condensação de vapor de água a 1 atm, utilizando uma placa vertical mantida a 90 °C. A primeira configuração é uma única placa ver
Um tubo horizontal, com 50 mm de diâmetro externo e temperatura superficial de 34°C, está exposto a vapor de água a 0,2 bar. Estime a taxa de condensação e a taxa de transferência de calor por unidade
O condensador de uma planta de potência a vapor é constituído por uma matriz quadrada alinhada com 625 tubos, cada um com diâmetro de 25 mm. Considere condições nas quais o vapor de água saturado a 0,