Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 50

Uma placa vertical de 2   m   ×   2   m tem um lado exposto a vapor de água saturado a pressão atmosférica e o outro à água de resfriamento que mantém a temperatura da placa a 50 ° C .

(a) Qual é a taxa de transferência de calor para o refrigerante? Qual a taxa na qual o vapor condensa sobre a placa?

(b) Para placas inclinadas com um ângulo θ em relação à vertical, o coeficiente convectivo médio para a condensação na superfície superior, L ( i n c l ) , pode ser aproximado por uma expressão com a forma, h - L i n c l   ≈   c o s   θ 1 4 ⋅   h - L ( v e r t ) , sendo h - L ( v e r t ) o coeficiente médio para a orientação vertical. Estando a placa 2   m   ×   2   m inclinada de 45 ° em relação à normal, quais são as taxas de transferência de calor e de condensação?

Passo 1

Vamos lá! Nosso problema pede a taxa de transferência de calor para a placa e o mesmo para a mesma placa inclinada em um ângulo de 45 ° , mas antes não vamos esquecer do nosso velho esboço pra facilitar nosso problema.

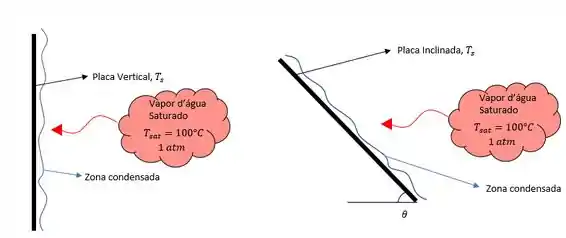
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)

I - P r o p r i e d a d e s   c o n s t a n t e s

Passo 2

(a)

Vamos lá! Iremos usar os dados da tabela A - 6 para água liquida saturada e água vapor saturado a 1   a t m , a equação 10.27 nos dá:

h f g ' = h f g + 0,68 c p , l T s a t - T s

h f g ' = 2400 k J k g

P = k l L T s a t - T s u l h f g ' v l 2 g 1 3 = 0,68 8 W m ⋅ K ⋅ 2   m ⋅ 100 - 50 ° C 3 7 5 ⋅ 10 - 6   N ⋅ s m 2 ⋅ 2 400 ⋅ 10 3 J k g ⋅ 3 , 8 5 ⋅ 10 - 7   m s 2 9,8   m s 2 1 3

P = 3000

Como P > 2530 , temos da equação 10.4 5 :

h - L v e r t = k l v l 2 g 1 3 ⋅ 1 P 0,0 , 24 P + 53 P r l 1 2 + 89 4 3  

h - L v e r t = 5220 W m 2 ⋅ K

Agora pra matar essa vamos lá, só substituir os valores para equação de taxa transferência de calor, assim temos:

q = h - L ( v e r t ) π D L T s a t - T S = 5220   W m 2 ⋅ K ⋅ 2 m ⋅ 2 m ⋅ 1 00 - 50 ° C  

q = 1,04 ⋅ 10 6   W

Como a taxa de condensação é dada por:

m ˙ = q h f g '

m ˙ = 0,435 k g s

Passo 3

(b)

Como h - L i n c l   ≈   c o s   θ 1 4 ⋅   h - L ( v e r t ) , temos que:

h - L i n c l = c o s   45 ° 1 4 ⋅   5220 W m 2 ⋅ K

h - L i n c l = 4820 W m 2 ⋅ K

q i n c l = h - L i n c l π D L T s a t - T S = 4820   W m 2 ⋅ K ⋅ 2 m ⋅ 2 m ⋅ 100 - 50 ° C  

q i n c l = 964   k W

Como a taxa de condensação é dada por:

m ˙ i n c l = q i n c l h f g '

m ˙ i n c l = 0,4 02 k g s

Isso é tudo pessoal! \o/

Resposta

(a) q v e r t = 1,0 4 ⋅ 10 6   W ,   m ˙ v e r t = 0,4 35 k g s

(b) q i n c l = 964   k W ,   m ˙ i n c l = 0,402 k g s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

67. Vapor de água saturado a 1,5 bar condensa no interior de um tubo horizontal com 75 mm de diâmetro, cuja superfície é mantida a 100°C. Supondo baixas velocidades no escoamento do vapor e um process
76. Um recipiente cilíndrico de paredes delgadas, com diâmetro D e altura L, contém, até uma altura y, um líquido (A) com baixo ponto de ebulição, que se encontra a Tsat,A. O recipiente está localizad
75. Uma seção de condensação–ebulição contém uma placa de cobre, com dimensões de 2 m × 2 m, que opera a uma temperatura uniforme de Ts = 100°C e separa vapor de água saturado, em condensação, de um l
74. Um esquema inovador para o resfriamento de chips de computadores utiliza um termossifão contendo um fluorocarboneto saturado. O chip é soldado no fundo de um recipiente com uma forma parecida com
66. O Ato do Ar Limpo (Clean Air Act) proibiu a produção de clorofluorocarbonos (CFCs) nos Estados Unidos a partir de 1996. Um CFC amplamente usado, refrigerante R-12, foi substituído pelo R-134a em m