Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 6
Considere condições de regime estacionário na condução unidimensional em uma parede plana com uma condutividade térmica e espessura , sem geração interna de calor.
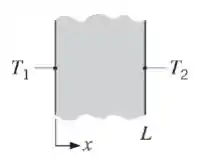
Determine o fluxo térmico e a grandeza desconhecida em cada caso e esboce a distribuição de
temperaturas, indicando o sentido do fluxo térmico.
Passo 1
Opa, tudo bem?
Vem comigo resolver essa questão!
Bora lá!
Começamos o nosso problema obtendo a relação utilizada para calcular o gradiente de temperatura:
Substituindo o valor de :
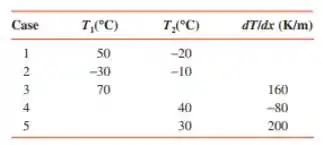
Agora, vamos analisar os casos propostos:
Passo 2
Caso 1:
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Passo 3
Caso 2:
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Passo 4
Caso 3:
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Passo 5
Caso 4:
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Passo 6
Caso 5:
Calculando o gradiente de temperatura:
Calculando o fluxo de calor:
Até a próxima questão!