Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 138
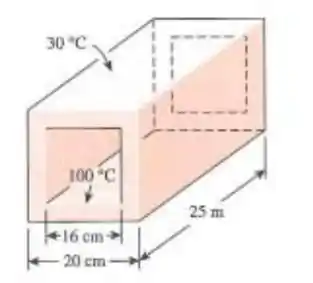
Considere um duto de concreto de seção transversal quadrada com 25 m de comprimento. As dimensões externas do duto são e a espessura da parede do duto é de 2 cm. Considerando que as superfícies interna e externa do duto estão a 100°C e 30°C, respectivamente, determine a taxa de transferência de calor através das paredes do duto.
Passo 1
Shoow galera, vamos começar a colocar a mão na massa !!
Já sabemos que o calor entre duas superfícies é dado por:
Já sabemos que:
Agora só precisamos calcular o S, o fator de forma de condução.
E como vamos calcula-lo?
Isso vai depender, porque para um tubo quadrado nós precisamos da razão
Se:
Então:
Como usamos:
Já temos que:
Então:
Na fórmula do calor:
E é só isso, galeraa !!
Resposta
Exercícios de Livros Relacionados
Um tubo com 50m m de diâmetro tem uma temperatura superficial de 85 ° C e está inserido no plano central de uma placa de concreto com 0,1m de espessura, cujas superfícies superior e inferior estão a 2
Uma fornalha de formato cúbico, com dimensões externas de 0,35m , é construída com tijolos refratários. Sendo a espessura da parede igual a 50m m , a temperatura da superfície interna igual a 600 ° C
Rejeitos radioativos são temporariamente armazenados em um recipiente esférico, cujo centro encontra-se enterrado a uma distância de 10m abaixo da superfície da terra. O diâmetro externo do recipiente
Água quente a 85 ° C escoa através de um tubo de cobre com parede delgada e diâmetro de 30m m . O tubo encontra-se no interior de uma casca cilíndrica excêntrica, mantida a 35 ° C e com diâmetro de 12
Transferência de calor por convecção natural é as vezes quantificada escrevendo-se a Equação 4.20 na forma q c o n v = S k e f ∆ T 1 – 2 , na qual k e f é a condutividade térmica efetiva. A razão k e