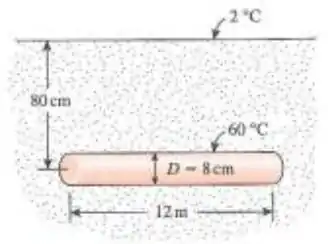
Um tubo de água quente de 12 m de comprimento e 8 cm de diâmetro, do sistema de aquecimento urbano, é enterrado no solo a 80 cm abaixo da superfície. A temperatura da superfície externa do tubo é de 60°C. Tomando a temperatura da superfície da terra como sendo 2°C e a condutividade térmica do local como sendo , determine a taxa de perda de calor do tubo.

Shoow galera, vamos começar a colocar a mão na massa !!

Já sabemos que o calor entre duas superfícies é dado por:

Já sabemos que:

Agora só precisamos calcular o S, o fator de forma de condução.

E como vamos calcula-lo?

Vamos olhar a geometria, certo?

Se temos um cilindro enterrado em um meio semi-infinito, nós podemos usar a fórmula:

Onde z é a profundidade.

Se:

Então:

Na fórmula do calor:

E é só isso, galeraa !!