Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 47
Considere o escoamento isentrópico de um fluido através de um bocal convergente-divergente e velocidade subsônica na garganta. Como a seção divergente afeta (a) a velocidade, (b) a pressão e (c) a vazão em massa do fluido?
Passo 1
Oi, galera, tudo beleza? Vamos fazer um exercício de escoamento subsônico (escoamento com velocidade é menor que a velocidade do som ) através de um bocal convergente-divergente?
Para resolver esse problema precisamos responder três perguntas na ordem abaixo.
- O que acontece com a velocidade do fluido conforme ele passa pela parte divergente do bocal (parte em que área transversal aumenta)?
- O que acontece com a pressão do fluido conforme ele passa pela parte divergente do bocal? Pela figura abaixo vemos que explicar o que acontece com a pressão do fluido através da parte divergente é o mesmo que dizer como essa pressão varia com a distância em relação a garganta.
- O que acontece com a vazão em massa do fluido conforme ele passa pela parte divergente do bocal? Pela figura abaixo vemos que explicar o que acontece com a vazão mássica do fluido através da parte divergente é o mesmo que dizer como essa como essa vazão mássica varia com a distância em relação a garganta.
Lembrando que: a velocidade do fluido através do bocal é menor que a velocidade do som e o número de Mach é menor que , porque o escoamento é subsônico!
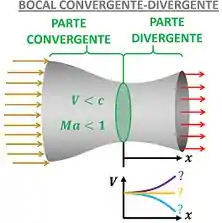
Pela figura acima vemos que explicar o que acontece com a velocidade do fluido através da parte divergente é o mesmo que dizer como essa velocidade varia com a distância em relação a garganta. Ou seja, precisamos saber se aumenta, diminui ou fica constante.
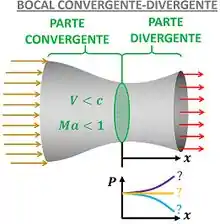
Em outras palavras, precisamos saber se aumenta, diminui ou fica constante.
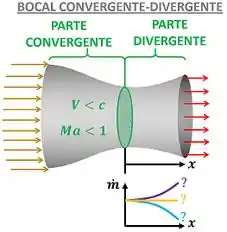
Em outras palavras, precisamos saber se aumenta, diminui ou fica constante.
A estratégia que usaremos para responder cada pergunta está listada abaixo.
- Para descobrir como varia, temos que usar a equação de conservação de massa e a equação da vazão mássica para a parte divergente do bocal.
- Para descobrir como varia, temos que usar a equação de Bernoulli na parte divergente do bocal.
- Para descobrir como varia, temos que usar a equação de conservação de massa.
Passo 2
Vamos resolver nesse passo a letra (a) da questão! Falamos que para descobrir como a velocidade do fluido varia, temos que usar duas equações. Uma delas é a lei da conservação de massa, que diz que a vazão mássica que entra na parte divergente tem que ser igual a vazão em massa que sai da parte divergente. A outra é a equação da vazão mássica, que diz que a vazão mássica é a multiplicação entre , e .
onde é a densidade do fluido entrando na parte divergente, é a densidade do fluido saindo da parte divergente, é a área de entrada da parte divergente (área menor), é a área de saída da parte divergente (área maior), é a velocidade de entrada do fluido e é a velocidade de saída do fluido.
Reorganizando a equação acima, encontramos uma expressão para a velocidade .
Como a área de entrada é menor que a área de saída , é menor que . Isso significa que a velocidade diminui confome o fluido atravessa o parte divergente do bocal.
Passo 3
Nessa etapa, vamos resolver a letra (b) dessa questão. Vimos que para descobrir como a pressão do fluido se comporta através do bocal, temos que usar a equação ode Bernoulli abaixo. Atenção! Nós podemos usar essa equação apenas para saber como varia, não para fazer cálculos e descobrir quanto exatamente vale. Bernoulli não é uma equação feita para ser usada em escoamentos compressíveis como é o caso agora!
onde é a pressão de entrada do fluido na parte divergente e é a pressão de saída do fluido da parte divergente.
Reorganizando a equação acima, achamos uma expressão para .
Como a velocidade do fluido é maior que a velocidade , vemos que é maior que . Isso significa que a pressão do fluido aumenta conforme ele atravessa a parte divergente do bocal.
Passo 4
Por sim, resolvemos a letra (c) da questão.
Para descobrir como a vazão mássica do fluido se comporta através da parte divergente do bocal, temos que usar a lei de conservação de massa.
A equação acima mostra que a vazão mássica que entra na parte divergente é igual a vazão em massa que saindo da parte divergente. Logo, se mantém constante através da parte divergente do bocal!
Resposta
- A velocidade do fluido diminui confome o fluido atravessa o parte divergente do bocal.
- A pressão do fluido aumenta conforme ele atravessa a parte divergente do bocal.
- se mantém constante através da parte divergente do bocal!