Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 38
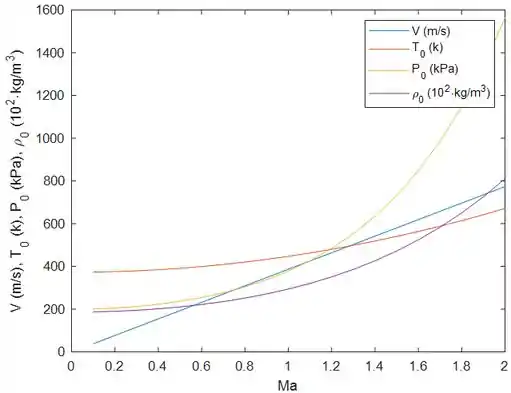
Reconsidere o Problema 12-37. Usando o EES (ou outro software), estude o efeito dos números de Mach no intervalo entre e sobre velocidade, pressão de estagnação, temperatura e massa específica do ar. Faça um gráfico de cada parâmetro como função do número de Mach.
Passo 1
O Problema 12-38 pede para a gente calcular quatro propriedades do ar a , que escoa através de um duto com um número de Mach que varia entre e . Essas propriedades são: a velocidade do ar , a temperatura de estagnação , a pressão de estagnação e a densidade de estagnação . A figura abaixo mostra os dados que temos e as informações que o enunciado pede.
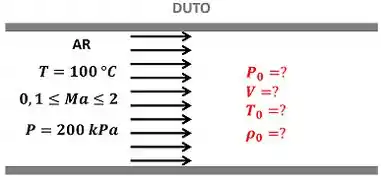
onde é a temperatura estática do ar e é a pressão estática do ar.
Para aprender a calcular essas propriedades , , e a partir do número de Mach , precisamos deduzir equações de , , e em função do número de Mach .
No próximo passo vamos aprender a deduzir essa equação para a velocidade do ar.
Passo 2
Para calcular a velocidade do ar, precisamos usar a equação do número de Mach (equação 12-12 do livro).
onde é a velocidade do som no ar.
A equação acima mostra que precisamos encontrar o valor da velocidade do som no ar para calcular .
A equação de para um gás ideal (o ar pode ser considerado um gás ideal) é a equação 12-11 do livro.
onde é a razão de calores específicos (no caso do ar, vale ) e é a constante do gás (no caso do ar ).
Cuidado! Essa temperatura tem que sempre estar em kelvin para o cálculo dar certo. Para fazer a converção de grau Celsius para Kelvin usamos a fórmula abaixo.
Substituindo essa fórmula na equação de , achamos:
Para fazer um gráfico de em função do número de Mach que varia entre e , calculamos o valor de para vários valor de que estão entre e . Ou seja, calcularemos o valor de para , depois calcularemos para e assim por diante até chegarmos em .
Passo 3
Com os valores de velocidade calculados para cada número de Mach , podemos calcular a temperatura de estagnação do ar a partir da equação 12-4 do livro.
onde é o calor específico a pressão constante (no caso do ar, ).
Além disso, calculamos a pressão de estagnação do ar a partir de , usando a equação 12-5 do livro.
Passo 4
Por fim, a densidade do ar pode ser deduzida a partir da equação de gás perfeito.
Através desse valor de densidade somos capazes d ecalcular a densidade de estagnação do ar , usando a equação 12-6 do livro.
Passo 5
Precisamos desenhar uma curva para cada propriedade , , e . Essas curvas são formadas por pontos com diferentes valores de . Logo, precisamos calcular , , e para vários valores de entre e . Em outras palavras, temos que repetir todo esse processo de cálculo para cada . Para fazer isso mais rápido, usamos o algoritmo abaixo e executamos esse algoritmo com o programa MATLAB.
Passo 6
O gráfico abaixo mostra todas as propriedades que o enunciado queria. Ele foi gerado a partir do algoritmo do MATLAB.
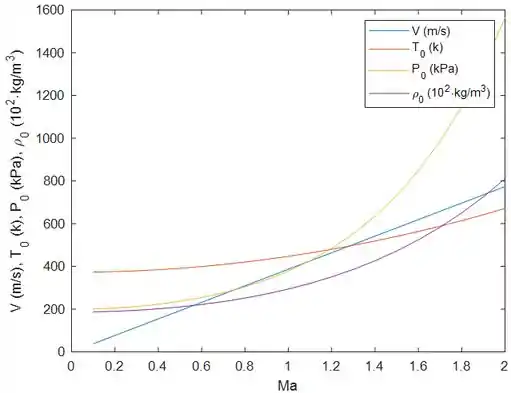
Resposta
