Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 81

Considere o escoamento de ar supersônico que se aproxima do nariz de uma cunha bidimensional ao número de Mach 5 . Usando a Figura 12-41, determine o ângulo de choque mínimo e o ângulo de deflexão máximo que um choque oblíquo direto pode ter.

Passo 1

Fala, galera! Como está o estudo de escoamentos compressíveis e onda de choque oblíquoa? Essa questão quer saber dois valores:

  1. Primeiro, ela pede o valor do ângulo de choque β mínimo que a onda de choque tem.
  2. Depois, ela pede o valor o ângulo de deflexão θ máximo que o fluido pode ter, quando atravessa o choque.

Para entender melhor o que são esses ângulos β e θ , a figura abaixo mostra esses termos.

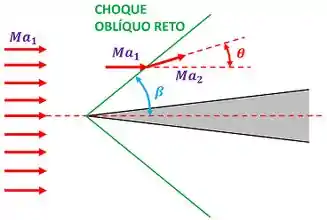
Pela figura acima vemos o ângulo de choque β é o ângulo entre o choque oblíquo e a direção que o escoamento tinha antes de passar pelo choque. Também vemos que o ângulo de deflexão θ mede a variação de direção de escoamento do fluido. Antes do choque ele se movimentava em uma direção e depois do choque ele passou a se movimentar em outra.

O M a 1 é o número de Mach que o fluido tinha antes de passar pelo choque. O valor de M a 1 vai ser fundamental para a gente encontrar β mínimo e θ máximo. No nosso caso, o enunciado informou que M a 1 vale:

M a 1 = 5

Já M a 2 é o número de Mach do fluido após ele passar pelo choque oblíquo. Ele é irrelevante para este problema.

Para achar tanto β mínimo quanto θ máximo teremos que usar o gráfico abaixo. Ele mostra várias curvas azuis com o número de Mach constante.

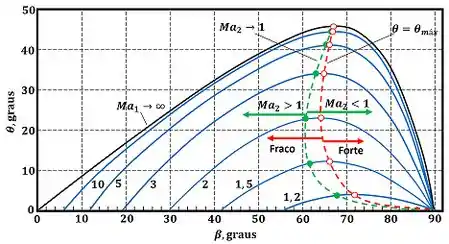
No próximo passo nós vamos aprender a usar essa figura e vamos achar os valores de β máximo e θ mínimo.

Passo 2

A figura acima mostra todos os valores possíveis do ângulo de choque β e do ângulo de deflexão θ para um determinado valor M a 1 do escoamento. Ou seja, uma vez que a gente descobre o valor de M a 1 , sabemos todos os valores possíveis de β e θ que um escoamento através de um choque oblíquo pode ter. Na figura abaixo, a curva relativa a M a 1 = 5 está ressaltada.

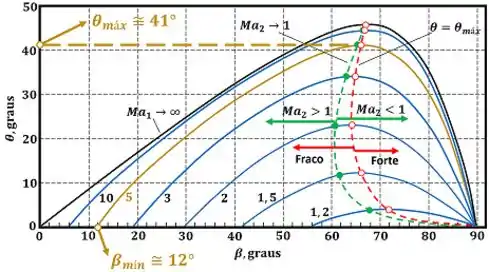
Nós vemos pela figura acima que o valor mínimo do ângulo de choque β é encontrado no cruzamento entre a curva de M a 1 = 5 (curva dourada) e o eixo x (eixo de β ). Podemos ver que o valor mínimo de β β m í n é aproximadamente:

β m í n ≅ 12 °

O valor do ângulo de deflexão pode ser encontrado localizando o topo da curva de M a 1 = 5 . Podemos ver que esse valor máximo θ m á x é aproximadamente:

θ m á x ≅ 4 1 °

Resposta

β m í n ≅ 12 °

θ m á x ≅ 41 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 12-92 considerando que o ar é resfriado na quantidade de 55k J / k g .
Ar entra em um duto sem atrito com V 1 = 70m / s , T 1 = 600K , e P 1 = 350k P a . Deixando a temperatura de saída T 2 variar de 600 a 5.000K , avalie a variação da entropia a intervalos de 200K , e f
Ar é aquecido à medida que escoa de modo subsônico através de um duto. Quando a quantidade de transferência de calor atinge 60k J / k g , observa-se que o escoamento é estrangulado, e que a velocidade
Qual é o aspecto característico do escoamento de Fanno? Quais são as principais hipóteses associadas ao escoamento de Fanno?
As relações isentrópicas dos gases ideais se aplicarão aos escoamentos através de (a) ondas de choque normais, (b) ondas de choque oblíquas e (c) ondas de expansão de Prandtl-Mcyer?