Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 60

12-60 Ar a 900   k P a e 400   K entra em um bocal convergente com velocidade desprezível. A área de garganta do bocal é de 10 c m 2 . Considerando o escoamento isentrópico, calcule e faça um gráfico da pressão de saída, a velocidade de saída e a vazão em massa versus a contrapressão P b for 0,9 ≥ P b ≥   0,1   M P a .

Passo 1

Vamos lá! O problema quer que a gente relacione a pressão de saída, velocidade de saída, e vazão mássica com a contrapressão P b em um intervalo de 0,9 ≥ P b ≥   0,1   M P a .

Isso por meio de um gráfico, ou seja, vamos ter 3 gráficos!

O problema diz pra a gente que a velocidade do ar é desprezível quando ele entra no bocal, então podemos dizer que a pressão e temperatura são de estagnação!

Esse esqueminha mostra pra a gente o que esta acontecendo:

Ok, mas vamos lá! A gente tem que fazer:

P e × P b

V e × P b

m ˙ m a x × P b

Para isso a gente vai fazer uma tabelinha para organizar todos os dados e depois montar os gráficos!

Mas primeiro temos que ver como vamos relacionar esses dados com os dados que o problema nos deu!

Passo 2

Em um bocal convergente vamos ter o seguinte comportamento, quando a contrapressão, P b for maior ou igual que a pressão crítica, P * teremos:

P b ≥ P * → P e = P b

E quando a contrapressão for menor que a pressão crítica:

P b < P * → P e = P *

Sabendo dessas relações já dar pra ter uma ideia de como vamos fazer o nosso primeiro gráfico! Precisamos descobrir P * !

Sabemos que P b varia de 0,9 ≥ P b ≥   0,1   M P a . Vamos passar para a mesma unidade que P 0 ?!

900 ≥ P b ≥ 100   k P a

Para descobrimos P * fazemos:

P * = P 0 2 k + 1 k k - 1  

Temos que descobir primeiro quem é P * , para o ar k = 1,4 :

P * = 900 k P a 2 1,4 + 1 1,4 1,4 - 1 = 475,5   k P a  

Temos:   900 ≥ P b ≥ 100   k P a e precisamos definir os pontos!

Eu escolhi fazer de 100 em 100   k P a e P b = P * , se você tiver com disposição pode usar um intervalo menor! Hahaha

Até agora podemos completar uma parte da nossa tabela:

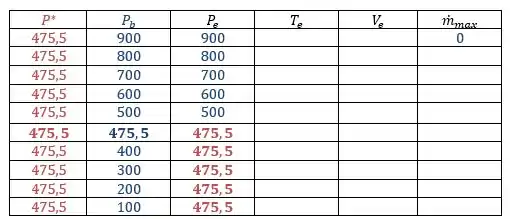
A primeira linha é referente ao ponto de estagnação, quando V e = 0 , como dado no enunciado!

Com essa tabela já podemos montar o primeiro gráfico!

Passo 3

Nosso próximo gráfico relaciona a velocidade V com P b , podemos descobrir a velocidade com a seguinte fórmula:

V = 2 c p T 0 - T e

Temos T 0 , mas precisamos encontrar T e , para isso fazemos:

T e = T 0 P e P 0 k - 1 k

Então vamos nessa!!

Para P e = 900   k , T e = 400   K que são os pontos de estagnação que o problema da pra a gente, então vamos começar a calcular a partir de P e = 800   k P a !

Para P e = 800   k P a :

T e = 400 800 900 1,4 - 1 1,4 = 386,8   K

Para os próximos valores a unica coisa que vai mudar é P e até a gente chegar em P * e depois disso T e vai permanecer constante, então aqui eu vou só preencher a tabelinha e você pode conferir sua resposta com a minha! Beleza?!

Passo 4

Agora podemos finalmente calcular V e com os dados de T e que terminamos de calcular.

V = 2 c p T 0 - T e

Para P e = 900   k P a a velocidade é V 0 = 0 , então podemos começar de P e = 800   k P a .

c p é tabelado, mas precisamos converter sua unidade

c p = 1,005 k J k g × K × 10 3   m 2 s 2 1 k J k g = 1,005 × 10 3 m 2 s 2 K

Então vamos começar:

V e = 2 × 1,005 × 1 0 3 × (   400 - 386,8 ) = 162,9   m / s

Daqui pra frente o que muda é T e , você só tem que olhar na tabelinha lá em cima e substituir! Vou deixar a tabelinha atualizada aqui em baixo!

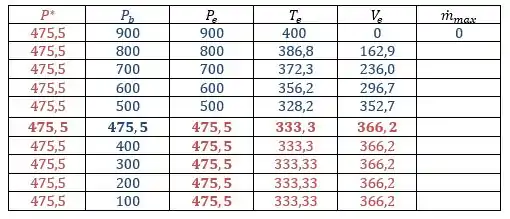
Podemos montar o segundo gráfico!!

Passo 5

Para o próximo gráfico a a gente tem que calcular m ˙ m a x :

m ˙ m a x = ρ e V e A e

A e é dado no enunciado:

A e = 10   c m 2 = 1 × 10 - 3 m 2

Para achar ρ e :

ρ e = P e R T e

Podemos substituir ρ e e ficar com:

m ˙ m a x = P e R T e V e A e

Aqui a gente tem que mudar P e ,   T e e V e a cada conta, mas não tem erro é só dar uma olhadinha na tabela do passo anterior!

R é tabelado, para o ar ele é R = 0.287 k P a   m 3 k g   K , como a pressão também esta em k P a não precisamos converter!

Para P e = 900 k , V e = 0 então m ˙ m á x = 0 , vamos então calcular o próximo ponto, para P e = 800 k !

m ˙ m a x = 800 0.287 × 386,8 162,9 × 1 0 - 3 = 1,174   k g / s

Daqui pra frente é só substituir P e , T e e V e de acordo com a tabelinha do passo anterior, fazendo o mesmo calculo para todos os pontos, temos:

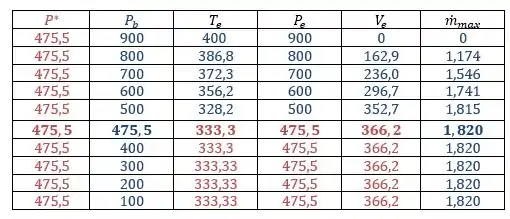
Agora finalmente o último gráfico! Uhuuuul!!!

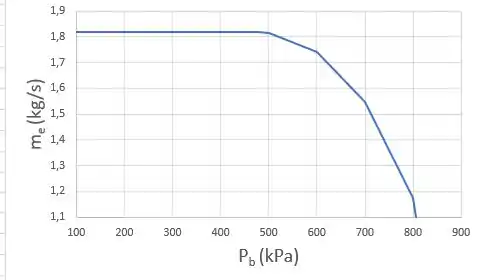
Aweeee!!!Cabôooo!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o aspecto característico do escoamento de Rayleigh? Quais são as principais hipóteses associadas ao escoamento de Rayleigh?
Em um diagrama T-s do escoamento de Rayleigh, o que representam os pontos na linha de Rayleigh?
Qual é o efeito do ganho de aquecimento e perda de calor sobre a entropia do fluido durante o escoamento de Rayleigh?
Ar que escoa a P 1 = 40k P a , T 1 = 280K e M a 1 = 3,6 é forçado a passar por uma curva de expansão de 15 ° . Determine o número de Mach, a pressão e temperatura do ar após a expansão.
Reconsidere o Problema 12-83. Determine o número de Mach a jusante, a pressão e temperatura abaixo da cunha para um choque oblíquo forte e número de Mach a montante de 5 .