Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 96
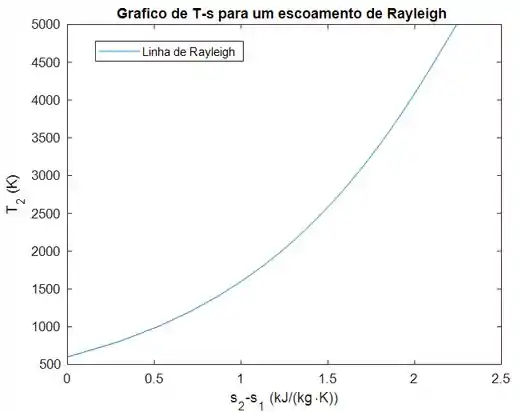
Ar entra em um duto sem atrito com , , e . Deixando a temperatura de saída variar de a , avalie a variação da entropia a intervalos de , e faça um gráfico da linha de Rayleigh em um diagrama T-s.
Passo 1
A questão é sobre um escoamento de Rayleigh do ar através de um duto. Nessa questão, as condições de entrada são fixas (ou seja, a pressão, temperatura e velocidade de entrada não mudam). No entanto, as condições de saída do ar variam. Sua temperatura de saída varia de até . Essa variação em causa uma variação na entropia de saída .
O problema quer que a gente calcule o quanto a entropia variou desde a entrada até a saída para várias temperaturas de saída diferentes. Em outras palavras, o problema quer saber variação de entropia para vários valores de . Além disso, ele quer que a gente desenhe um gráfico de versus , mostrando os resultados. Esse gráfico é a linha de Rayleigh.
A figura abaixo mostra os dados que temos e a informação que a questão pede.
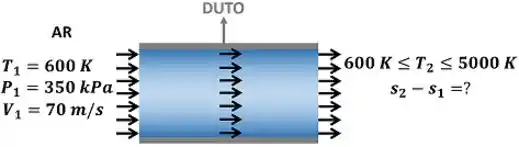
, e são a pressão, a temperatura e a velocidade do ar respectivamente.
O ar pode ser considerado um gás ideal com calor específico constante . Por isso, podemos calcular através da fórmula de variação de entropia para um gás ideal com constante que se encontra abaixo.
é a constante de gás do ar e vale . é a pressão de saída do ar.
No próximo passo vamos aprender como usar essa fórmula!
Passo 2
Nesse passo, vamos aprender a usar a fórmula de variação de entropia para gases ideais. Para usar essa fórmula, precisamos conhecer todos os termos do lado direito da questão. No entanto, não sabemos quanto vale a pressão de saída do ar . Para calcular esse valor, usamos uma equação que relaciona a pressão que temos com a pressão que não temos.
onde é o número de Mach do ar na entrada, é o número de Mach do ar na saída e é uma constante que vale para o ar.
Com essa fórmula, aprendemos a calcular a razão que aparece na equação de através de dois termos que ainda não conhecemos, mas que sabemos calcular: e .
pode ser encontrado, juntando duas equações: equação número de Mach abaixo
com a equação da velocidade do som de gases ideais abaixo.
onde é a velocidade do som na entrada.
Substituindo na equação de :
O número de Mach de entrada tem um único valor , porque as condições de entrada do ar são constantes. No entanto, como as condições de saída do ar variam, o número de Mach de saída terá um valor para cada valor de .
Esses valores de podem ser calculados, resolvendo a equação de abaixo.
Aplicando a raiz quadrada nos dois lados da equação e reorganizando a fórmula, achamos a equação de segundo grau abaixo (polinômio de segundo grau, sendo a variável independente).
Para ficar mais claro que a equação abaixo é uma equação de segundo grau, podemos substituir por e reconhecer os coeficientes , e do polinômio.
A equação acima quer dizer que é uma das raízes da equação de segundo grau acima. Ela é a raiz real e positiva .
Isso quer dizer que, para achar , devemos aplicar a fórmula de Bhaskara (aquela que você falou que nunca usaria pra nada na sua vida, se lembra?).
Note que, a partir da equação acima, vamos encontrar uma raiz real, maior ou igual a zero e menor ou igual a 1 (que é o valor de ) para cada valor de entre e . A questão pede para a gente variar de em . Ou seja, calcularemos primeiro o valor de para , depois para e assim por diante até chegar no último valor para .
Por fim, utilizaremos cada valor de para calcular vários valores de e substituiremos os encontrados na fórmula de . Esses valores finais de formarão a linha de Rayleigh!
No próximo passo aprenderemos a fazer esses cálculos repetidos de uma forma mais rápida!
Passo 3
No passo anterior nós vimos a quantidade enorme de cálculos repetidos que precisamos fazer para gerar o gráfico de versus . Como podemos fazer isso de uma forma mais rápida?
Programando um algoritmo para fazer as contas automaticamente para a gente!
Abaixo, nós vemos um algoritmo do MATLAB feito para realizar essas contas!
No próximo passo veremos os resultados.
Passo 4
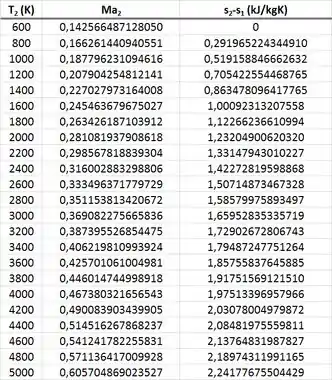
Nesse passo, será mostrado o gráfico T-s ( versus ) gerado pelo algoritmo do MATLAB e a tabela gerada por esse algoritmo também.
Segue abaixo o gráfico, mostrando o aumento da variação de entropia com o aumento de .
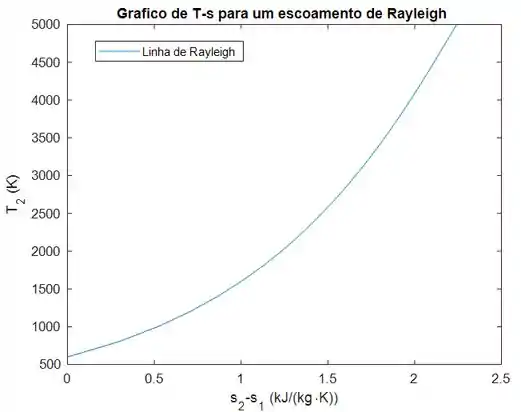
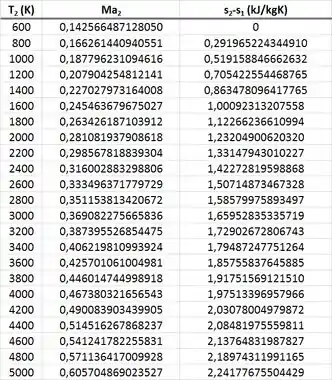
A tabela também mostra esse aumento de com a temperatura de saída .
Resposta
