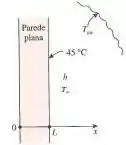
Considere uma extensa parede plana de espessura e condutividade térmica . Não há acesso ao lado interno da parede em , por isso as condições térmicas nessa superfície são desconhecidas. Entretanto, sabe-se que a superfície externada da parede em , cuja emissividade é , troca calor por convecção com ar ambiente em temperatura , com coeficiente médio de transferência de calor , bem como por radiação com as superfícies ao redor, que se encontram a uma temperatura média . Além disso, a temperatura da superfície externa mede . Assumindo que a transferência de calor é unidimensional e permanente, (a) expresse a equação diferencial e as condições de contorno para condução de calor através da placa, (b) obtenha a relação para temperatura da superfície externa da placa resolvendo a equação diferencial e (c) avalie a temperatura da superfície interna da parede em .

Agora, precisamos resolver a nossa EDO e utilizar as condições de contorno, pois, determinar a variação de temperatura na parede nada mais é do que determinar a distribuição de temperatura nela. Portanto, temos:

Aplicando ambas as condições de contorno, temos o seguinte sistema:

Resolvendo o sistema, vamos obter a seguinte equação para a distribuição de temperatura:

Substituindo os valores das constantes, temos:

E esta é a distribuição de temperatura na parede.

Por fim, vamos obter a temperatura na superfície interna da parede. Substituindo na equação que descobrimos no Passo 2, temos:

E é isto aí!