Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 83

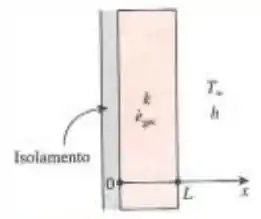
Considere uma extensa placa de espessura L e condutividade térmica k na qual calor é gerado uniformemente a uma taxa de e ˙ g e r . Um dos lados da placa está isolado, euqnato o outro está exposto a um ambiente de temperatura T ∞ com coeficiente de transferência de calor h . (a) Expressa a equação diferencial e as condições de contorno para condução de calor unidimensional permanente através da placa, (b) determine a variação da temperatura na placa e (c) obtenha as relações para as temperaturas de ambas as superfícies e o aumento máximo de temperatura na placa por parâmetros fornecidos.

Passo 1

O nosso primeiro passo é fazer considerações para resolver o nosso problema. Sendo assim, temos um problema de regime permanente, com condução de calor unidimensional, geração de calor e condutividade térmica constante.

Como estamos trabalhando com uma placa, vamos utilizar o sistema de coordenadas retangular. Portanto, a EDO que rege o nosso problema é:

d 2 T d x 2 + e ˙ g e r k = 0

Agora, precisamos discutir as condições de contorno que o nosso problema está sujeito, os quais são dois. O primeiro é a parede isolante. Isto quer dizer que não há fluxo de calor quando x = 0 (percebam que estamos utilizando o sistema de coordenadas do desenho da questão). Desta forma, temos:

- k d T d x x = 0 = 0

Já a outra é condução de calor na outra superfície igual a convecção do fluido. Portanto, temos:

- k d T d x x = L = h T s - T ∞

Passo 2

Agora, precisamos resolver a nossa EDO e utilizar as condições de contorno, pois, determinar a variação de temperatura na placa nada mais é do que determinar a distribuição de temperatura nela. Portanto, temos:

d 2 T d x 2 = - e ˙ g e r k

d T d x = - e ˙ g e r k x + C 1

T x = - e ˙ g e r 2 k x 2 + C 1 x + C 2

Agora, precisamos utilizar as condições de contorno para descobrir quem são as constantes que apareceram na nossa equação. Primeiro, para a parede isolante, temos:

- k d T d x x = 0 = - k - e ˙ g e r k ⋅ 0 + C 1 = - k C 1 = 0

C 1 = 0

Agora, para a outra parede, temos:

- k d T d x x = L = h T s - T ∞

- k - e ˙ g e r k ⋅ L = h T s - T ∞

T s = T ∞ + e ˙ g e r h L

Lembrando que T s = T L , descobrimos que:

T L = - e ˙ g e r 2 k L 2 + C 2 = T ∞ + e ˙ g e r h L

C 2 = e ˙ g e r 2 k L 2 + T ∞ + e ˙ g e r h L

Portanto, a distribuição de temperatura na placa é:

T x = - e ˙ g e r 2 k x 2 + e ˙ g e r 2 k L 2 + T ∞ + e ˙ g e r h L

E é isto ai!

Passo 3

Estamos quase terminando a nossa questão! Agora, precisamos determinar as temperaturas em ambas as superfícies e o aumento máximo de temperatura.

Começando pela temperatura das superfícies, percebam que já temos uma delas calculada, que é a temperatura T s ! Ela é:

T L = T s = T ∞ + e ˙ g e r h L

Já para obtermos a temperatura na superfície isolante basta substituir x = 0 na equação T ( x ) . Com isto, obtemos:

T 0 = e ˙ g e r 2 k L 2 + T ∞ + e ˙ g e r h L = e ˙ g e r 2 k L 2 + T s

E o aumento máximo é a diferença entre essas duas temperaturas calculadas. Portanto,

Δ T m á x = T 0 - T L = e ˙ g e r 2 k L 2

Resposta

  1. A EDO é:

    2. d 2 T d x 2 + e ˙ g e r k = 0

    E as condições de contorno são:

    - k d T d x x = 0 = 0

    - k d T d x x = L = h T s - T ∞

  2. A distribuição de temperatura na placa é:

    3. T x = - e ˙ g e r 2 k x 2 + e ˙ g e r 2 k L 2 + T ∞ + e ˙ g e r h L

  3. As temperaturas nas superfícies são:

T L = T s = T ∞ + e ˙ g e r h L

T 0 = e ˙ g e r 2 k L 2 + T ∞ + e ˙ g e r h L = e ˙ g e r 2 k L 2 + T s

Já o aumento máximo de temperatura é:

Δ T m á x = T 0 - T L = e ˙ g e r 2 k L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Informa-se que a condutividade térmica de uma folha de isolante extrudado rígido é igual a k = 0,029W / ( m.K ) . A diferença de temperaturas medida entre as superfícies de uma folha com 20m m de espe
As temperaturas interna e externa de uma janela de vidro com 5m m de espessura são 15 e 5 ° C . Qual é a perda de calor através de uma janela com 1m x 3m ? A condutividade térmica do vidro é de 1,4W /
A laje de concreto de um porão tem 11m de comprimento, 8m de largura e 0,20 m de espessura. Durante o inverno, as temperaturas são normalmente de 17 ° C e 10 ° C em suas superfícies superior e inferio
O fluxo térmico através de uma lâmina de madeira, com espessura de 50m m , cujas temperaturas das superfícies interna e externa são 40 e 20 ° C , respectivamente, foi determinado, sendo igual a 40W /
Uma câmara de congelador é um espaço cúbico de lado igual a 2m . Considere que a sua base seja perfeitamente isolada. Qual é a espessura mínima de um isolamento à base de espuma de estireno ( k = 0,03