Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 84

Um longo fio de resistência homogênea, raio r 0 = 0,6   c m e condutividade térmica k = 15,2   W / m ⋅ K está sendo usado para ferver água em pressão atmosférica pela passagem da corrente elétrica. Calor é gerado no fio uniformemente como resultado do aquecimento da resistência a uma taxa de 16,4   W / c m 3 . O calor gerado é transferido para a água a 100   ° C por convecção, e o coeficiente médio de transferência de calor é h = 3200   W / m 2 ⋅ K . Considerando uma transferência de calor permanente unidimensional, (a) expresse a equação diferencial e as condições de contorno para condução de calor através do fio, (b) obtenha a relação para a variação de temperatura no fio, resolvendo a equação diferencial, e (c) determine a temperatura na linha central do fio.

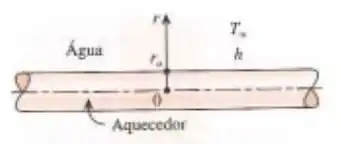
Passo 1

O nosso primeiro passo é fazer considerações para resolver o nosso problema. Sendo assim, temos um problema de regime permanente, com condução de calor unidimensional, geração de calor e condutividade térmica constante.

Como estamos trabalhando com um fio de formato cilíndrico, vamos utilizar o sistema de coordenadas cilíndrica. Portanto, a EDO que rege o nosso problema é:

1 r d d r r d T d r + e ˙ g e r k = 0

Agora, precisamos discutir as condições de contorno que o nosso problema está sujeito, os quais são dois. O primeiro é a simetria do fio. Esta simetria implica em dizer que a temperatura máxima do fio está localizada no meio dele. Consequentemente, não há condução de calor em r = 0 . Portanto:

- k d T d r r = 0 = 0

Já a outra é condução de calor na outra superfície igual a convecção do fluido. Portanto, temos:

- k d T d r r = r 0 = h T s - T ∞

Passo 2

Agora, precisamos resolver a nossa EDO e utilizar as condições de contorno, pois, determinar a variação de temperatura na placa nada mais é do que determinar a distribuição de temperatura nela. Portanto, temos:

1 r d d r r d T d r = - e ˙ g e r k

r d T d r = - e ˙ g e r 2 k r 2 + C 1

Vamos utilizar a nossa primeira condição de contorno, a simetria do problema. Com isto, temos:

d T d r r = 0 = 0

Logo,

r d T d r = 0 = 0 - e ˙ g e r 2 k 0 2 + C 1

C 1 = 0

Agora que descobrimos o valor da primeira constante, vamos continuar a resolver a nossa EDO. Portanto:

r d T d r = - e ˙ g e r 2 k r 2

d T d r = - e ˙ g e r 2 k r

T r = - e ˙ g e r 4 k r 2 + C 2

Precisamos utilizar a nossa segunda condição de contorno. Portanto, temos:

- k d T d r r = r 0 = h T s - T ∞

- k - e ˙ g e r 2 k r 0 = h T s - T ∞

T s = T ∞ + e ˙ g e r 2 h r 0

Lembrando que T s = T r 0 , descobrimos que:

T r 0 = - e ˙ g e r 4 k r 0 2 + C 2 = T ∞ + e ˙ g e r 2 h r 0

C 2 = e ˙ g e r 4 k r 0 2 + T ∞ + e ˙ g e r 2 h r 0

Portanto, a distribuição de temperatura no nosso fio é:

T r = - e ˙ g e r 4 k r 2 + e ˙ g e r 4 k r 0 2 + T ∞ + e ˙ g e r 2 h r 0

Vamos substituir todos os valores agora, para expressar numericamente a nossa função! Com isto, temos:

T r = - 16,4 ⋅ 10 6 4 ⋅ 15,2 r 2 + 16,4 ⋅ 10 6 4 ⋅ 15,2 0,006 2 + 100 + 16,4 ⋅ 10 6 2 ⋅ 3200 0,006

T r = - 2,697 ⋅ 10 5 ⋅ r 2 + 125,08

OBS: Tomem muito cuidado na hora de substituírem os valores, por causa das unidades!

Passo 3

Estamos quase terminando a nossa questão! Agora, basta descobrirmos a temperatura na linha central do fio. E isto é o nosso passo mais fácil agora! Basta pegarmos a função T r encontrada anteriormente e substituir o valor r = 0 nela. Com isto, temos:

T 0 = - 2,697 ⋅ 10 5 ⋅ 0 2 + 125,08

T 0 = 125,08   ° C

Resposta

  1. A EDO é:

    2. 1 r d d r r d T d r + e ˙ g e r k = 0

    E as condições de contorno são:

    - k d T d r r = 0 = 0

    - k d T d r r = r 0 = h T s - T ∞

  2. A distribuição de temperatura na placa é:

    3. T r = - e ˙ g e r 4 k r 2 + e ˙ g e r 4 k r 0 2 + T ∞ + e ˙ g e r h L

    Ou

    T r = - 2,697 ⋅ 10 5 ⋅ r 2 + 125,08

  3. A temperatura na linha central é:

T 0 = 125,08   ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calor é perdido a uma taxa de 275 W por m 2 de área de parede de 15 cm de espessura com condutividade térmica de k = 1,1W / m ⋅ K . A queda de temperatura através da parede é:37,5 °C27,5 °C16,0 °C8,0
165 – Considere uma placa de circuito multicamada de 18c m × 18c m dissipando 27W de calor. A placa é composta por quatro camadas de 0,2m m de espessura de cobre k = 386 W m ⋅ K e três camadas de 1,5m
Considere um pequeno objeto de metal aquecido de massa m e calor específico c que inicialmente está a uma temperatura T i . O objeto é resfriado em ambiente a uma temperatura T ∞ por convecção, com co
Gases de exaustão de uma fábrica estão sendo expelidos pela chaminé de exaustão de 10 m de altura, 1 m de diâmetro externo, 10 cm de espessura da parede e condutividade térmica de 40W / m ⋅ K . Os gas
Uma parede plana de espessura L = 4 cm tem condutividade térmica k = 20W / m ⋅ K . Uma reação química ocorre dentro da parede, resultando na geração de calor uniforme e uma taxa de e ˙ g e r = 10 5W /