Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 202

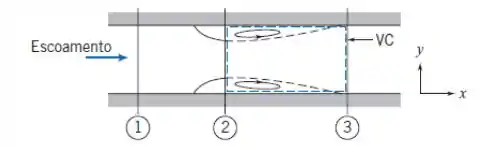
Considere a instalação de um bocal medidor em um tubo. Aplique as equações básicas ao volume de controle indicado, para mostrar que a perda de carga permanente através do medidor pode ser expressa, em forma adimensional, como o coeficiente de perda de carga,

C l = p 1 - p 3 p 1 - p 2 = 1 - A 2 / A 1 1 + A 2 / A 1

Trace um gráfico de C l como uma função da razão de diâmetros, D2/D1.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiro, temos:

Q = V 1 A 1 = V 2 A 2 = V 3 A 3

Aplicando a equação de Bernoulli, temos:

p 1 - p 2 ρ = V 2 2 - V 1 2 2 = V 2 2 2 1 - A 2 A 1 2 = V 2 2 2 1 - A 2 A 3 2

Agora, pelo usando somatório de forças para o momento e utilizando a continuidade, temos:

F s x = p 2 A 1 - p 2 A 3 = V 2 - ρ V 2 A 2 + V 3 - ρ V 3 A 3 = V 3 - V 2 ρ V 3 A 3 p 3 - p 2 ρ = V 3 V 2 - V 3 = V 2 A 2 A 3 V 2 - V 2 A 2 A 3 = V 2 2 A 2 A 3 1 - A 2 A 3

Passo 2

Para a energia, temos:

Q = u 2 + V 2 2 2 + p 2 ρ - ρ V 2 A 2 + u 3 + V 3 2 2 + p 3 ρ ρ V 3 A 3

Logo:

h l 23 = u 3 - u 2 - Q n = V 2 2 - V 3 2 2 - p 3 - p 2 ρ = V 2 2 2 1 - A 2 A 3 2 - p 3 - p 2 ρ

Agora, vamos assumir que h l 12 ≈ 0 , logo, h l 1 3 = h l 2 3 . Sendo assim, temos:

h l 1 3 = V 2 2 2 1 - A 2 A 3 2 - V 2 2 A 2 A 3 1 - A 2 A 3 h l 13 = V 2 2 2 1 - A 2 A 3 2

Podemos dividir esta equação por ( p 1 - p 2 ) / ρ . Fica assim:

C l = h l 13 p 1 - p 2 ρ C l = 1 - A 2 / A 3 1 + A 2 / A 3

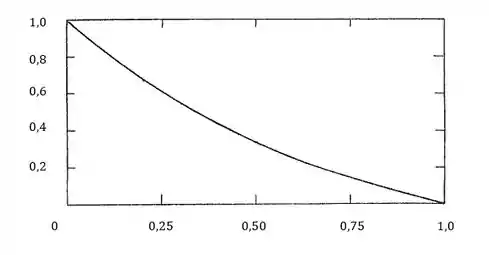
Com isso, podemos plotar o gráfico assim:

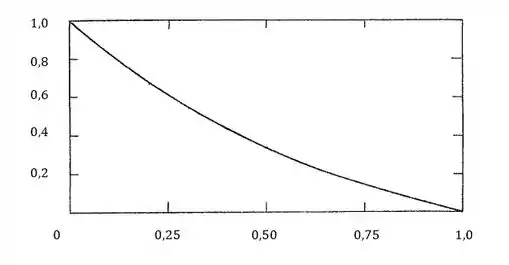
Onde:

A 2 A 1 = D 2 D 1 2

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo liso, de 200m de comprimento e diâmetro de 100m m , liga dois reservatórios (a entrada e a saída do tubo são de bordasvivas). No ponto médio do trecho de tubo está uma placa de orifício com di
A vazão volumétrica em um duto circular pode ser medida por um “pitot transverso”, isto é, pela medida da velocidade em vários segmentos de área através do duto, seguida do somatório das vazões segmen
Em alguns estados do oeste, água para mineração e irrigação era vendida por “polegada de mineiro”, ou seja, a taxa para a qual a água escoa através de uma abertura de 645m m 2 de área em uma tábua ver
Gasolina a 20°C escoa a 0,06m³/h por um tubo de 15 cm de diâmetro e é medida por um medidor do tipo bocal de raio longo de 9 cm. Qual é a queda de pressão esperada através do bocal?
Um avião utiliza um tubo de Pitot estático como velocímetro. As medidas, com suas incertezas são: uma temperatura estática de - 11 ± 3 ° ° C , uma pressão estática de 60 ± 2k P a e uma diferença de pr