Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 53
Considere uma piscina com 4 m de comprimento, 4 m de largura e 1,5 m de altura acima do solo que está cheia de água até a borda, (a) Determine a força hidrostática de cada parede e a distância da linha de ação dessa força ao solo. (b) Se o peso das paredes da piscina dobrar e a piscina estiver cheia, a força hidrostática de cada parede dobrará ou quadruplicará? Por quê?
Passo 1
Oi pessoal, tudo bem?
Bem, inicialmente assumimos que:
- A pressão atmosférica atua nos dois lados da parede da piscina e, portanto, pode ser ignorada nos cálculos.
Consideramos que a densidade da água do lago é: .
E do problema, temos:
E podemos representar a ação da força resultante sobre a parede da piscina como:
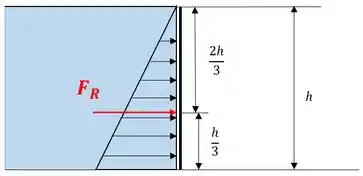
Passo 2
Letra a) A pressão média na superfície é a pressão no centróide (ponto médio) da superfície e é determinado como:
Substituindo os termos e resolvendo a equação:
Assim, a força hidrostática resultante em cada parede é:
A linha de ação da força passa pelo centro de pressão, a 2h/3 da superfície livre e h/3 do fundo da piscina. Portanto, a distância da linha de ação do solo é:
Letra b) Se a altura das paredes da piscina for dobrada, a força hidrostática quadruplica:
E assim a força hidrostática é proporcional ao quadrado da altura da parede, h².
À título de curiosidade: Esta é uma das razões pelas quais as piscinas acima do solo não são muito profundas, enquanto as piscinas no solo piscinas podem ser bastante profundas.
Resposta
Portanto:
Letra a) ;
Letra b) Se a altura das paredes da piscina for dobrada, a força hidrostática quadruplica. E assim a força hidrostática é proporcional ao quadrado da altura da parede, h².